Four identical coins are placed in a square. For each coin, the ratio of area to circumference is the same as the ratio of circumference to area. The area of the square not covered by the coins is

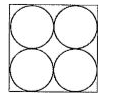
$16 (π - 1)$

$16 (8 - π)$

$16 (4 - π)$

$16 (4 - \frac{π}{2})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

Answer

Step by step video, text & image solution for Four identical coins are placed in a square. For each coin, the ratio of area to circumference is the same as the ratio of circumference to area. The area of the square not covered by the coins is by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.

Updated on:21/07/2023

Class 14 MATHS MENSURATION

Topper's Solved these Questions

Knowledge Check

If the ratio of areas of two circles is 4:9, then the ratio of their circumference will be :
A $3 : 2$
B $9 : 4$
C $2 : 3$
D $4 : 9$
The areas of two circles are in the ratio $9 : 4$ .The ratio of their circumferences is
A $3 : 2$
B $4 : 9$
C $2 : 3$
D $81 : 16$
The ratio of circumference and area of a circle is 2:7. Find the circumference.
A $14 π$
B $\frac{7}{π}$
C $7 π$
D $\frac{14}{π}$

DISHA PUBLICATION-MENSURATION-Practice Exercises (STANDARD LEVEL)

Home
Ask Doubt
Profile

Four identical coins are placed in a square. For each coin, the ratio of area to circumference is the same as the ratio of circumference to area. The area of the square not covered by the coins is

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

If the ratio of areas of two circles is 4:9, then the ratio of their circumference will be :

The areas of two circles are in the ratio 9:4.The ratio of their circumferences is

The ratio of circumference and area of a circle is 2:7. Find the circumference.

DISHA PUBLICATION-MENSURATION-Practice Exercises (STANDARD LEVEL)

The areas of two circles are in the ratio $9 : 4$ .The ratio of their circumferences is