Figure, ABCD is a square of side 2a. Find the ratio between the circumferences and the areas of the incircle and the circum-circle of the square.
Video Solution
Text Solution
The diameter of inner circle is 2a
The radius is a
The diameter of outer circle is 2√2a
Therefore radius of outer circle √2a
The circumference of inner circle is=2×π×2a=4×π×a
The circumference of outer circle is=2×π×√2a
ratio between the circumferences of the inner circle and outer circle= 4×π×a2×π×√2a=1:√2
The area of inner circle =π×(a)2=π×a2
The area of outer circle = π×(√2a)2=2×π×a2
ratio between the areas of the inner circle and outer circle= π×a22×π×a2=1:2
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The ratio of the area of the incircle and the circum-circle of a square is
A1:2B√2:1C1:√2D2:1The ratio of the areas of the incircle and the circumcircle of a square is-
A1:√2B1:√3C1:4D1:2The ratio of the areas of the incircle and circumcircle of a square is
A1:2B1:3C2::1DNone of these
ABCD is a square. Find out the side of square?
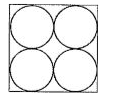
View SolutionFour identical coins are placed in a square. For each coin, the ratio of area to circumference is the same as the ratio of circumference to area.Find the area of the square that is not covered by the coins
View SolutionThe ratio of the areas of the incircle and circumcircle of a square is
View SolutionThe ratio of the areas of the circumcircle and the incircle of a square is
View SolutionFour identical coins are placed in a square. For each coin, the ratio of area to circumference is the same as the ratio of circumference to area. The area of the square not covered by the coins is
View Solution

