An elastic belt is placed round the rim of a pulled of radius 5cm. One point on the belt is pulled directly away from the centre of the pulley until it is at P, 10cm from O. Find the length of the belt that is in contact with the rim of the pulley. Also, find the shaded area.
Let
In
Arc AB =
Length of the belt that is in contact with the rim of the pulley
= Circumference of the rim -Length of arc AB
Length of the belt that is in contact with the rim of the pulley =
Area of sector OACB=
Area of quadrilateral OAPB = 2 (Area of )
Area of quadrilateral OAPB = cm^2
Shaded area = Area of quadrilateral OAPB - Area of sector OACB
Shaded area = =17.13 cm^2
Topper's Solved these Questions
Similar Questions
An elastic belt is placed around the rim of a pulley of radius 5 cm (Fig.) From one point C on the belt, the elastic belt is pulled directly away from the centre O of the pulley until it is at P, 10 cm from the point O. Find the length of the belt that is still in contact with the pulley. Also, find the shaded area.[use π=3.14 and √3=1.73]
View SolutionThe length of the tangent from an external point P to a circle of radius 5cm is 10cm. The distacne of the point from the centre of the circle is
View Solution
Knowledge Check
The length of the tangent drawn to a circle of radius 4 cm from a point 5 cm away from the centre of the circle is
A3cmB4√2 cmC5√2cmD3√2 cmA tangent PQ at a point P of a circle of radius 5cm meets a line through the centre O at a point Q so that OQ=13cm. Find the length of PQ.
A12 cmB7 cmC10 cmD15 cmThe length of a chord of a circle of radius 10 cm is 12 cm. Find the distance of the chord from the centre of the circle.
A6 cmB5 cmC8 cmD7 cm
A point P is at a distance of 29cm from the centre of a circle of radius 20cm. Find the length of the tangent drawn from P to the circle.
View SolutionA point is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
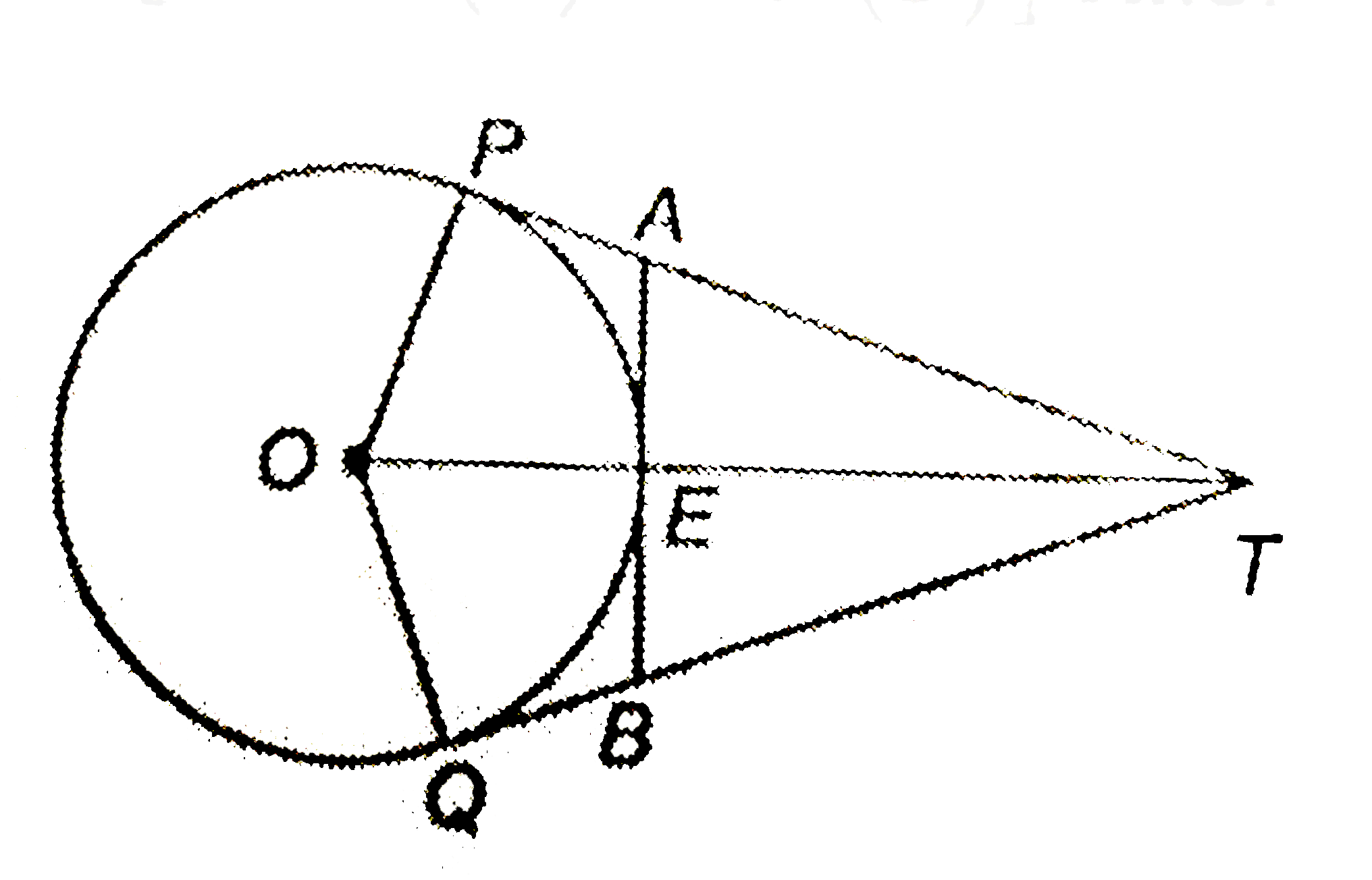
View SolutionO is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E, find the length AB.
View SolutionA chord of length 16cm is drawn in a circle of radius 10cm. Find the distnace of the chord from the centre of the circle.
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ=13cm . Find the length of PQ .
View Solution
