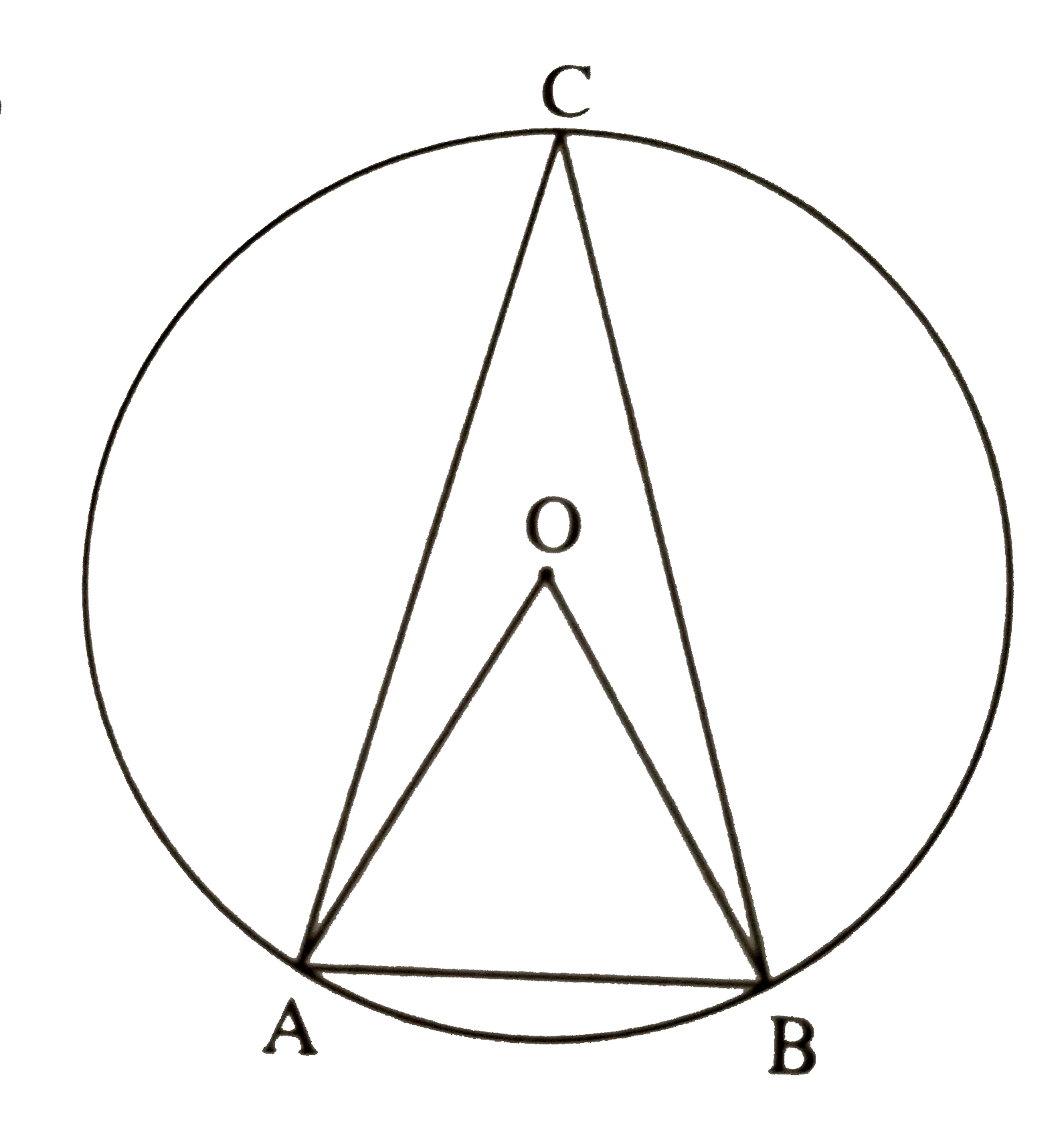
In a circle with centre O and radius 5cm, AB is a chord of length 5√3cm . Find the area of sector AOB.
Given: {AB}=5√3
⇒AL=BL=5√32
Assume, ∠AOB=20. So, ∠AOL=∠BOL=θ.
In △OLA,
sinθ=ALOA=5√325=√32
⇒θ=60∘
⇒∠AOB=120∘
⇒ Area of sector AOB
=120360×π×52cm2=25π3cm2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a circle with centre at O (0,0) 2. and radius 5 cm, AB is a chord of length 8 cm. If OM is perpendicular to AB, then the length of OM is:
A2.5cm.B3cm.C4cm.D1cm.There is a circle of radius 5 cm. There are two chords AB and AC OF equal length = 6 cm . Find the length of chord BC .
A4.8 cmB10.8cmC9.6 cmDnone of these
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm. Find the area of sector of the circle formed by chord AB .
View SolutionGiven a circle with centre O and radius 2.5 cm, what is the length of the longest chord of the circle
View SolutionAB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
View SolutionThe arc AB of the circle with centre at 'O' and: radius 10 cm has length 16 cm, What is the area of the sector bounded by the radii OA, OB and the arc AB ?
View SolutionIn the figure, in a circle with centre O, length of chord AB is equal to the radius of the circle. Find measure of each of the following.
∠AOB
View SolutionIn a circle of radius 5 cm, AB and AC are two chords such that AB=AC=6cm. Find the length of the chord BC
View Solution
