In the figure, in a circle with centre O, length of chord AB is equal to the radius of the circle. Find measure of each of the following.
$∠ A O B$

Video Solution

Text Solution

Verified by Experts

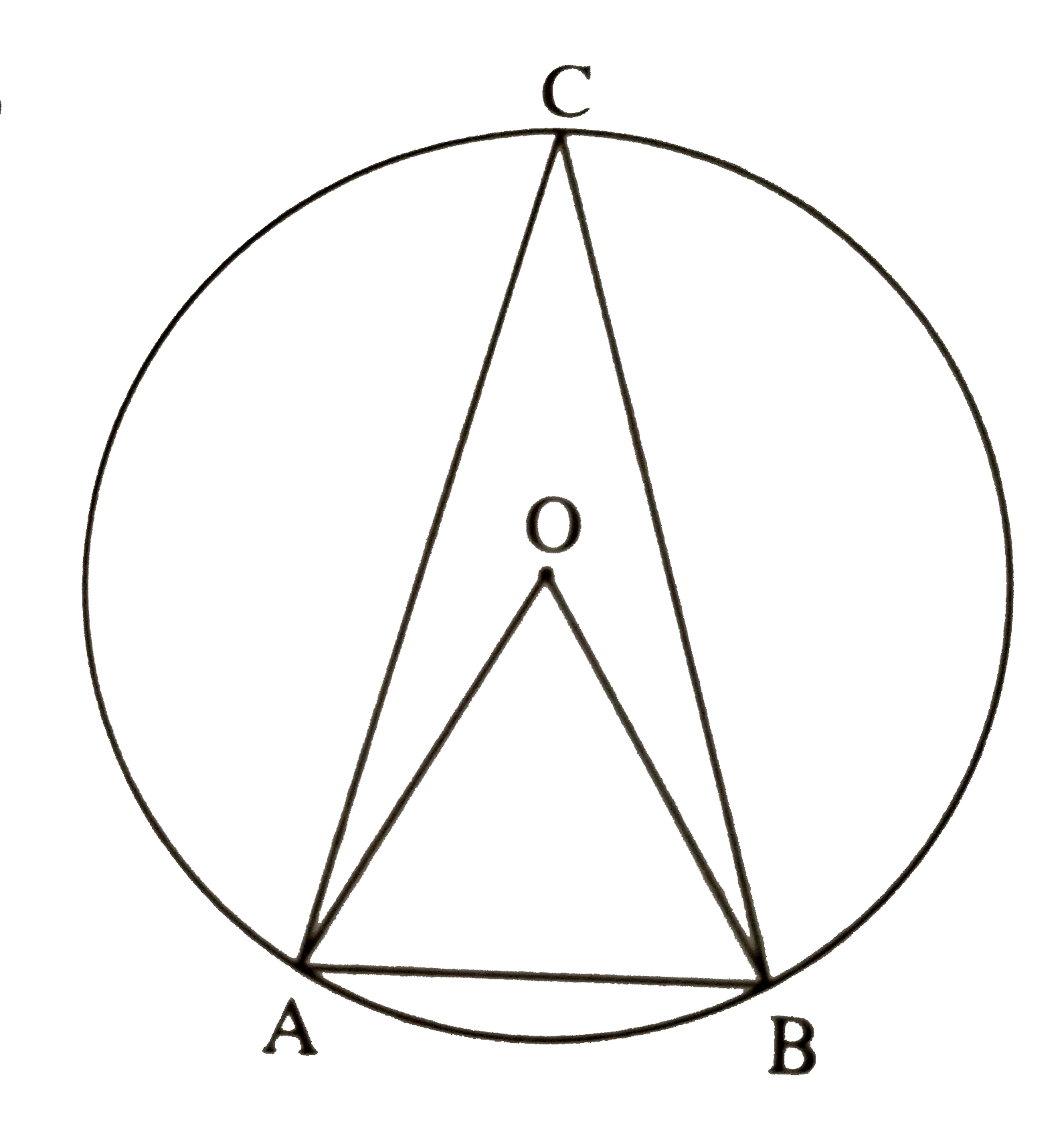
Seg OA $≅$ seg OB $\dots\dots\dots (Radii of the same circle)$
chord AB is equal to radius $\dots\dots.. (Given)$
$∴ S e g A B ≅ s e g O A ≅ s e g O B$
$∴ △ A O B$ is equoilateral
$∴ ∠ A O B = 60^{\circ} \dots\dots.. (Angle of an equilateral triangle)$

|

Updated on:21/07/2023

Class 10 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If the length of a chord AB is equal to the radius OA of the circle, then $∠ A B O$ equals (O is the center)

A $120^{\circ}$
B $60^{\circ}$
C $45^{\circ}$
D $30^{\circ}$
Question 2 - Select One
AB is a diameter of a circle with centre O. CD is a chord equal to the radius of the circle. AC and BD are produced to meet at P. Then the measure of $∠ A P B$ is:
A $120^{\circ}$
B $30^{\circ}$
C $60^{\circ}$
D $90^{\circ}$
Question 3 - Select One
AB is a chord in a circle with centre O. AB is produced to C such that BC is equal to the radius of the circle. C is joined to O and produced to meet the circle at D. If $∠ A C D = 32^{\circ}$ , then the measure of $∠ A O D$ is .......
A $48^{\circ}$
B $96^{\circ}$
C $108^{\circ}$
D $80^{\circ}$

NAVNEET PUBLICATION - MAHARASHTRA BOARD-CIRCLE-PRACTICE SET 3.4

Home
Ask Doubt
Profile