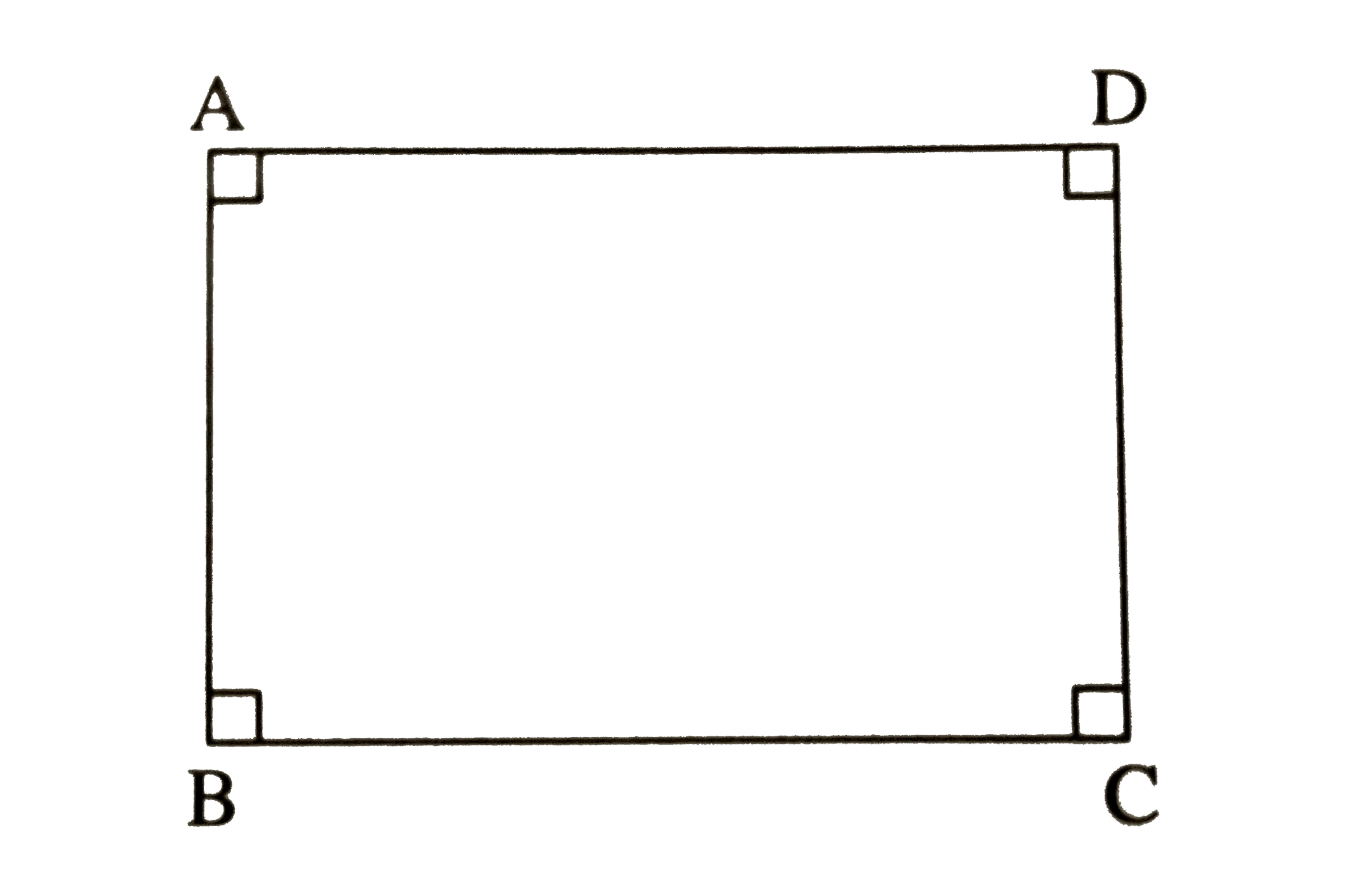
Prove that, any rectangle is a cyclic quadrilateral.

Video Solution

Text Solution

Verified by Experts

$□ A B C D$ is rectangle.
$□ A B C D$ is cyclic.
$□ A B C D$ is a rectangle. $\dots\dots. (Given)$
$∴ ∠ A = ∠ B = ∠ C = ∠ D = 90^{\circ} \dots\dots. (Angles of a rectangle)$
$∠ A + ∠ C = 90^{\circ} + 90^{\circ} = 180^{\circ}$
$∴ □ A B C D$ is cyclic $........ (By concerse of cyclic quadrilateral theorem)$

Updated on:21/07/2023

|

Class 10 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

The quadrilateral formed by the bisectors of the angles of a parallelogram is a

Arectangle
Bsquare
Cparallelogram
Dcyclic quadrilateral
The quadrilateral formed by the bisectors of the angles of a parallelogram is a

Arectangle
Bsquare
Cparallelogram
Dcyclic quadrilateral

NAVNEET PUBLICATION - MAHARASHTRA BOARD-CIRCLE-PRACTICE SET 3.4

Home
Ask Doubt
Profile