The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic.
Video Solution
Text Solution
Given: ABCD is a cyclic quadrilateral.
To prove: The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic.
Proof: AH, BF, CF and DH are the angle bisectors of ∠A, ∠B, ∠C and ∠D.
⇒∠FEH=∠AEB .......(1) [Vertically opposite angles]
⇒∠FGH=∠DGC .......(2) [Vertically opposite angles]
Adding (1) and (2),
⇒∠FEH+∠FGH=∠AEB+∠DGC .......(3)
Now, By angle sum property of a triangle,
⇒∠AEB=180∘−(12∠A+12∠B) ........ (4)
⇒∠DGC=180∘−(12∠C+12∠D) .......(5)
Substituting equation (4) and equation (5) in equation (3)
⇒∠FEH+∠FGH=180∘−(12∠A+12∠B)+180∘−(12∠C+12∠D)
⇒∠FEH+∠FGH=360∘−12(∠A+∠B+∠C+∠D)
⇒∠FEH+∠FGH=360∘−12×360∘
⇒∠FEH+∠FGH=180∘
Since The sum of opposite angles of quadrilateral EFGH=180∘
∴EFGH is a cyclic quadrilateral.
∴ The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The quadrilateral formed by the bisectors of the angles of a parallelogram is a
 ArectangleBsquareCparallelogramDcyclic quadrilateral
ArectangleBsquareCparallelogramDcyclic quadrilateralWhich of the following statements is/are correct?
The intersections of the angle bisectors of the quadrilateral are the vertices of the cyclic quadrilateral
If diagonals of a cyclic quadrilateral perpendicularly intersect at point P, then the line through P, perpendicular to any side bisects the opposite side.
The product of the lengths of the two diagonals of a cyclic quadrilateral is equal to the sum of the products of opposite sides.A(i) and (ii)B(ii) and (iii)C(i) and (iii)Dall of theseThe quadrilateral formed by the bisectors of the angles of a parallelogram is a
 ATrapeziumBKiteCRectangleDNone
ATrapeziumBKiteCRectangleDNone
Prove that, any rectangle is a cyclic quadrilateral.
View SolutionProve that, any rectangle is a cyclic quadrilateral.
View SolutionProve that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.
View SolutionABCD is a cyclic quadrilateral (see Figure). Find the angles of the cyclic quadrilateral.
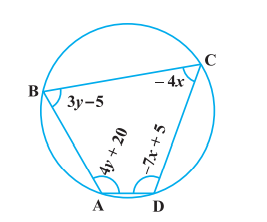
View SolutionThe bisectors of the angles formed by producing the opposite sides of a cyclic quadrilateral (provided that they are not parallel) intersect at right angle.
View Solution
