If O is the circumcentre of a ABC and OD⊥BC, prove that ∠BOD=∠A.
∴ O is the point of intersection of perpendicular bisectors of the sides of △ABC.
⇒D is the midpoint of BC
⇒BD=DC
In △OBD and △OCD,
OB=OC(Radius of circle)
OD=OD(Common)
BD=DC(Proved)
△OBD≅△OCD(SSS congruency criterion)
⇒∠BOD=∠COD (By CPCT )
⇒∠BOD=∠COD=12∠BOC
We know that the angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
⇒∠BOC=2∠BAC
⇒2∠BOD=2∠BAC (From equation (1))
⇒∠BOD=∠BAC
Hence Proved.
Topper's Solved these Questions
Similar Questions
If 'O' is the circum centre of the ABC and R1, R2, R3 are the radii of the circumcircle of triangle OBC, OCA and OAB respectively then aR1+bR2+cR3 has the value equal to abc2R3 (b) R3abc (c) 4R2 (d) abcR3
View SolutionBisector AD of ∠BAC of ABC passes through the centre O of the circumcircle of ABC as shown in figure. Prove that AB=AC.
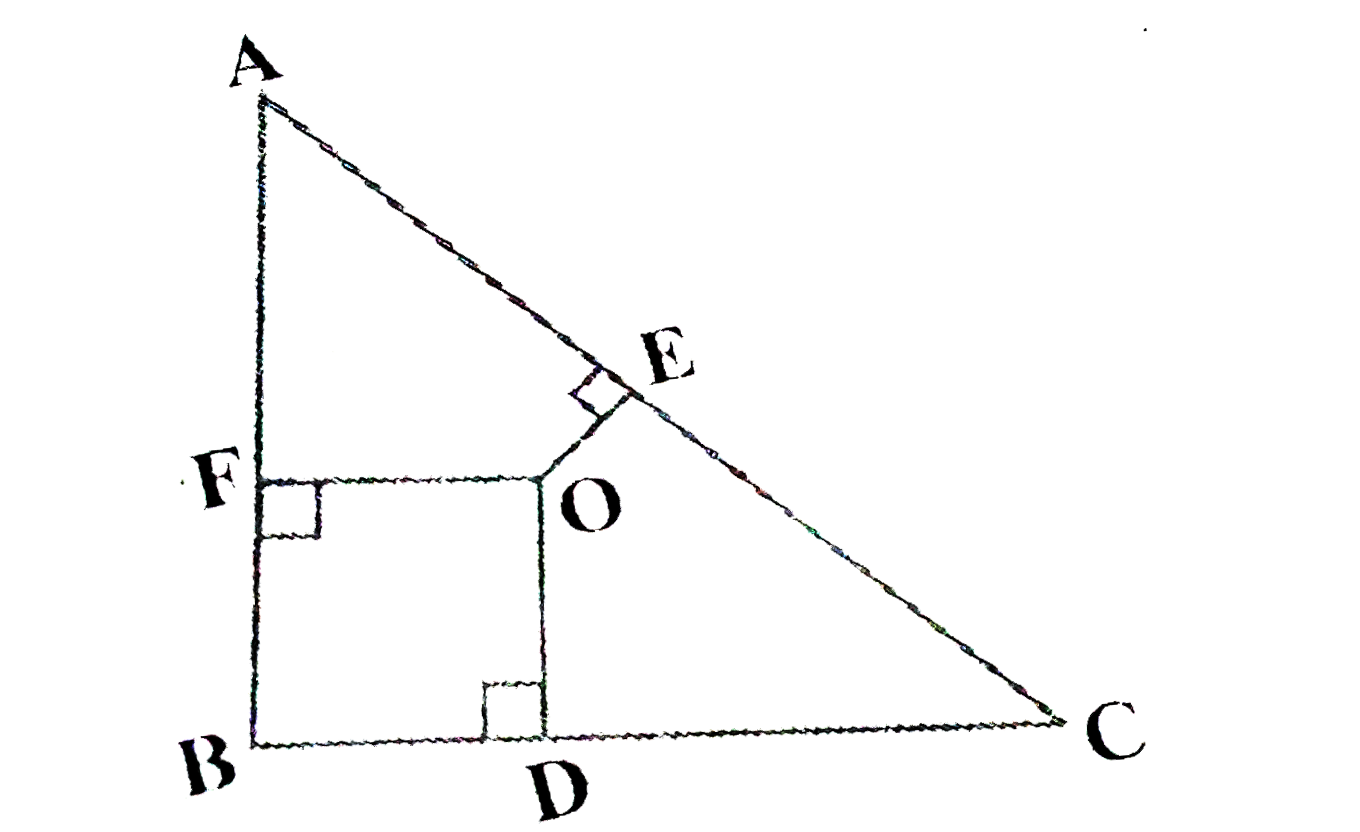
View SolutionIn figure, O is a point in the interior of a triangle ABC, OD⊥BC,OE⊥ACand OF⊥AB. Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AW2+CD2+BF2
View SolutionIf a<b and c≤d, prove that a+c<b+d
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(BOE)=18ar(ABC)
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE, prove that ar ( BOE)=18ar ( ABC)
View SolutionIf O and O′ are circumcentre and orthocentre of ABC, then →OA+→OB+→OC equals
a.2→OO' b. →OO' c. →O'O d. 2→O'O
View SolutionIn figure, ABC is triangle in which ∠ABC=90∘and AD⊥CBproduced. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A Line through O intersects AB at P and DC at Q. Prove that ar(△POA)=ar(△QOC).
View SolutionIn fig., O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that:- OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
View Solution
