In figure, O is a point in the interior of a triangle ABC, OD⊥BC,OE⊥ACand OF⊥AB. Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AW2+CD2+BF2
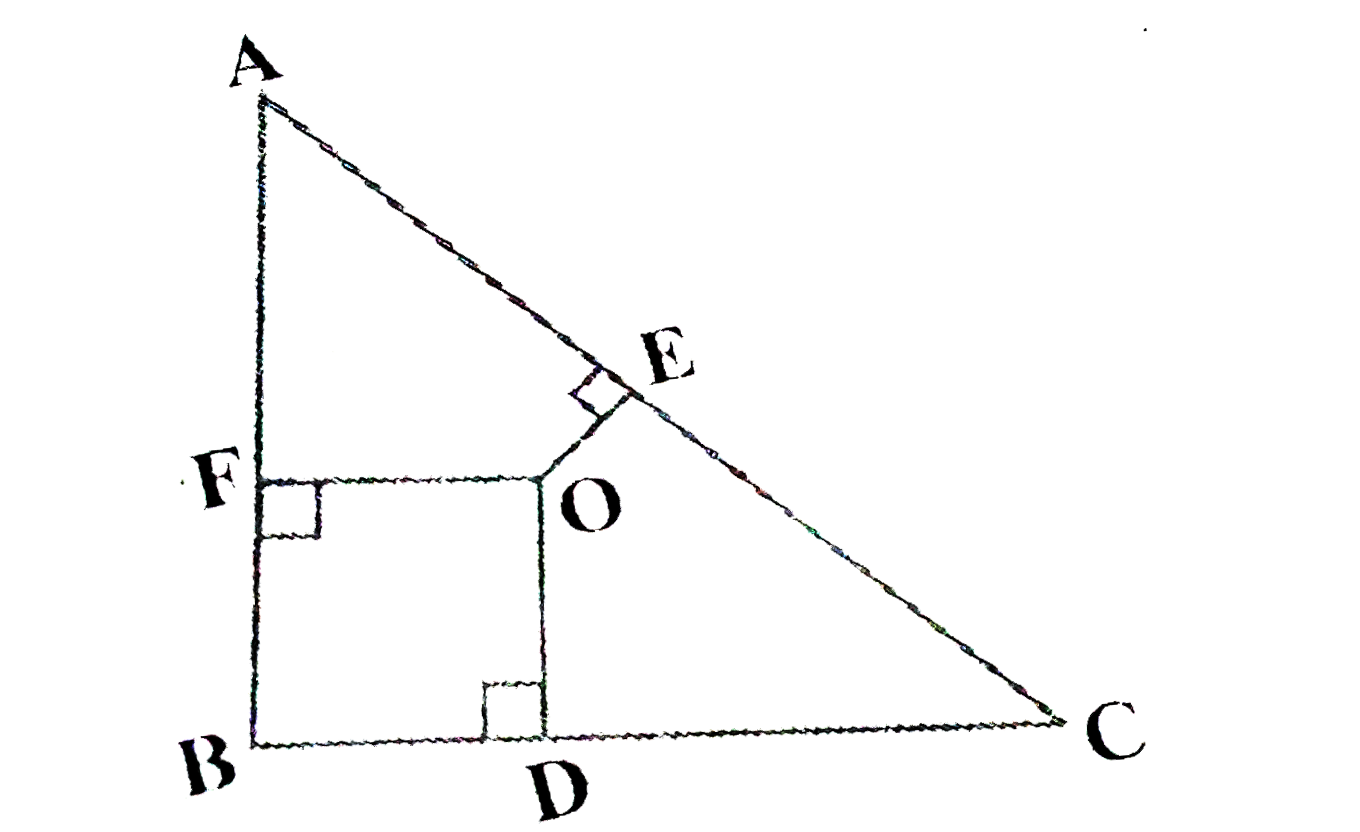
In △ABC
OD⊥BC, OE⊥AC, and OF⊥AB
OA, OB, and OC joined as shown below.
Using Pythagoras theorem, in ΔOAF,
OA2=AF2+OF2 [Since, ∠OFA=90∘]............... (1)
Similarly, In △OBD
OB2=BD2+OD2 [Since ∠ODA=90∘].............. (2)
In △OCE
OC2=CE2+OE2 [Since, ∠OEC=90∘]………………(3)
Adding equations (1), (2) and (3)
OA2+OB2+OC2=AF2+OF2+BD2+OD2+CE2+OE2
OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2............. (4)
(ii) From equation (4) let's rearrange and group the terms.
(OA2−OE2)+(OB2−OF2)+(OC2−OD2)=AF2+BD2+CE2
Since, △OAE, △OFB and △ODC are right triangles
Using pythagoras theorem we have,
AE2=OA2−OE2.............. (5)
BF2=OB2−OF2 .............. (6)
CD2=OC2−OD2............... (7)
AF2+BD2+CE2=AE2+CD2+BF2 [ From equations (5), (6) and (7)]]
Similar Questions
Knowledge Check
What is the chemical formula of Ozone ?
A. O
B. O2
C. O3
D. O4ABBACDDC
In ABC, ∠A=60o . Prove that B C^2=A B^2+A C^2-A B.A C .
View SolutionIn a quadrilateral ABCD , given that ∠A+∠D=90o . Prove that AC2+BD2=AD2+BC2 .
View SolutionIn figure, ΔODCΔOBA,∠BOC=125oand ∠CDO=70o. Find∠DOC,∠DCOand∠OAB.
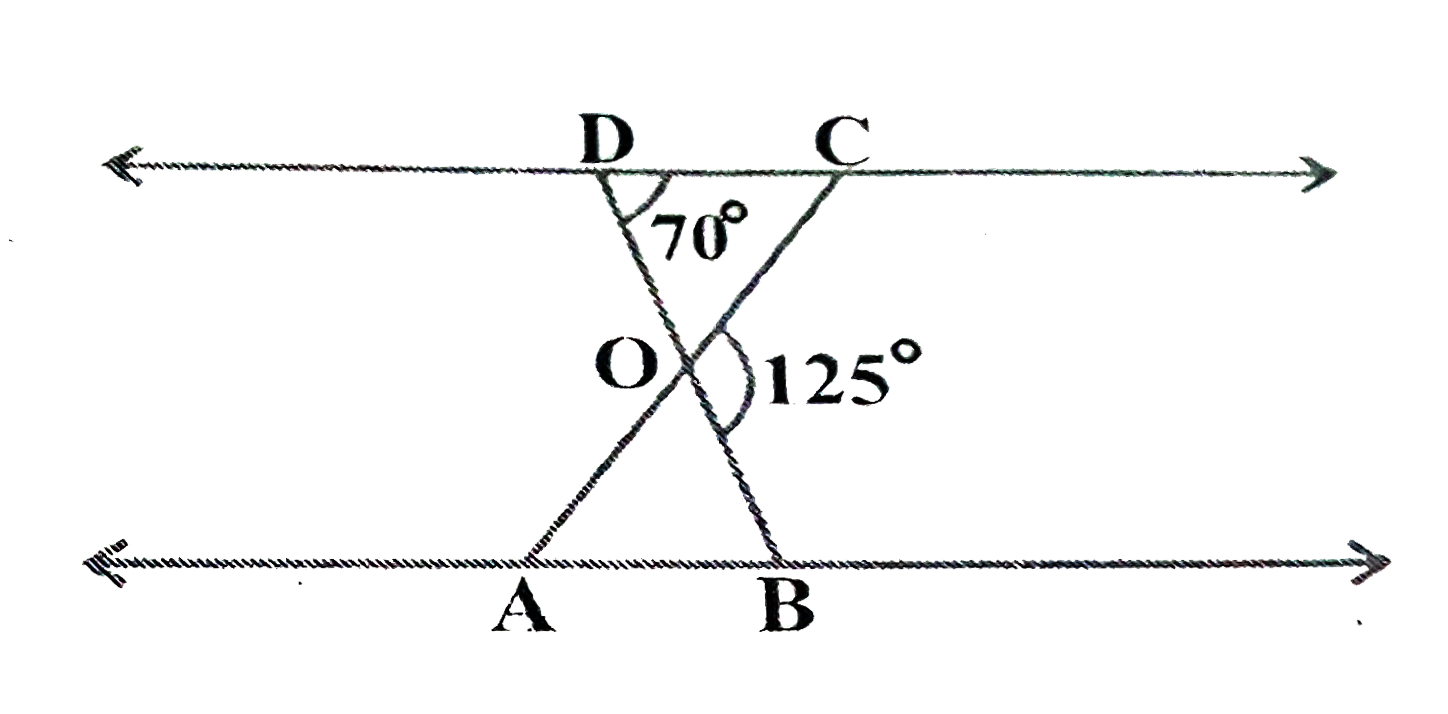
View SolutionABCD is a rectangle with O as any point in its interior. If ar (AOD)=3 cm2and ar (BOC)=6 cm2, then area of rectangle ABCD is: 9cm2 (b) 12 cm2 (c) 15cm2 (d) 18 cm2,
View SolutionABCD IS A PARALLELOGRAM AND O is any point in its interior. Prove that: ar (AOB)+ ar (COD)= ar (BOC)+ ar(AOD) ar (AOB)+ar (COD)=12 ar(^(gm)ABCD) Given: A parallelogram ABCD and O is a point in its interior. To Prove: ar ( AOB)+ ar(COD)=ar (BOC)+ar(AOD)
View SolutionThe AD,BEandCF are the medians of a cABC, then (AD2+BE2+CF2):(BC2+CA2+AB2) is equal to
View SolutionA point O inside a rectangle ABCD is joined to the vertices. Prove that the sum of the areas of a pair of opposite triangles so formed is equal to the sum of the other pair of triangles. GIVEN : A rectangle ABCD and O is a point inside it. OA,OB,OC and OD have been joined.. TO PROVE : ar(AOD)+ar(BOC)=ar(AOB)+ar(COD) CONSTRUCTION : Draw EOFAB and LOMAD.
View Solution

