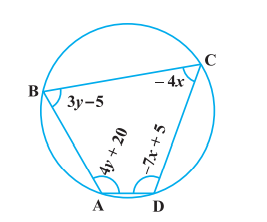
ABCD is a cyclic quadrilateral (see Figure). Find the angles of the cyclic quadrilateral.
Video Solution
Text Solution
We know that the opposite angles of a cyclic quadrilateral are supplementary
Hence, sum of the measures of opposite angles in a cyclic quadrilateral is180∘.
∠A+∠C=180∘
(4y+20)+(−4x)=180∘
4y+20−4x=180∘
−4(x−y)=160∘
x−y=−40∘....(1)
Also,∠B+∠D=180∘
(3y−5)+(−7x+5)=180∘
3y−5−7x+5=180∘
−7x+3y=180∘
7x−3y=−180∘ .... (2)
Multiplying equation (1) by 3, we obtain
3x−3y=−120∘ ....(3)
Subtracting equation (3) from equation (2), we obtain
(7x−3y)−(3x−3y)=−180∘−(−120)∘
4x=−60∘
x=−15∘
Substituting x=−15∘ in equation (1), we obtain
−15∘−y=−40∘
y=25∘
Therefore by using x=−15∘and y=25∘ we have,
∠A=4y+20=4×25+20=120∘
∠B=3y−5=3×25−5=70∘
∠C=−4x=−4×(−15)=60∘
∠D=−7x+5=−7×(−15)+5=110∘
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The quadrilateral formed by the bisectors of the angles of a parallelogram is a
 ArectangleBsquareCparallelogramDcyclic quadrilateral
ArectangleBsquareCparallelogramDcyclic quadrilateralThe quadrilateral formed by the bisectors of the angles of a parallelogram is a
 ArectangleBsquareCparallelogramDcyclic quadrilateral
ArectangleBsquareCparallelogramDcyclic quadrilateral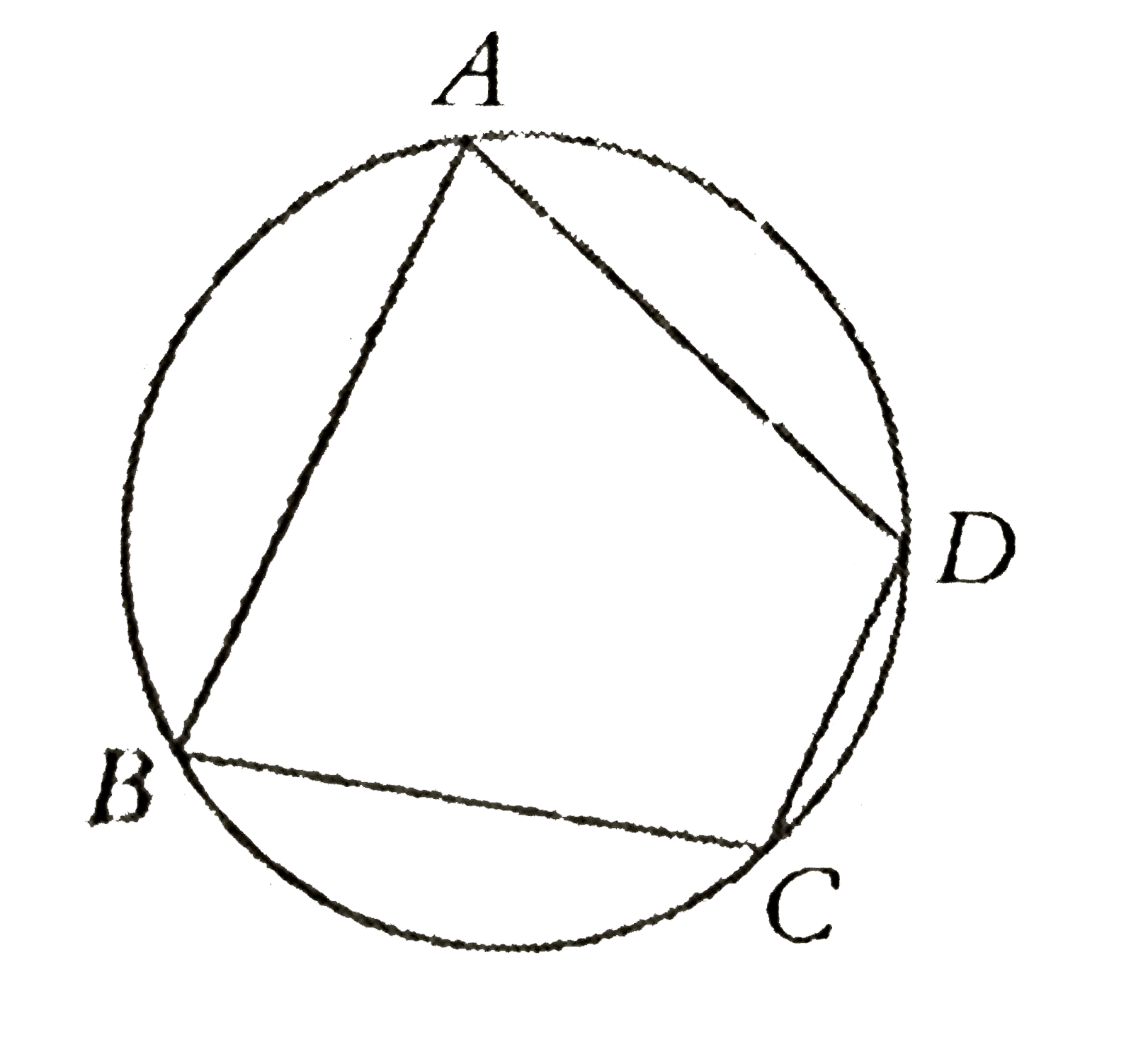
In the above figure, ABCD is a cyclic quadrilateral and ∠BCD=2∠BAD. Find the angle made by the diagonal BD at the centre of the circle.A60∘B80∘C100∘D120∘
Definition of Cyclic quadrilateral
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.

View Solution
In the above figure, ABCD is a cyclic quadrilateral and ∠BCD=2∠BAD. Find the angle made by the diagonal BD at the centre of the circle.
View SolutionProve that, any rectangle is a cyclic quadrilateral.
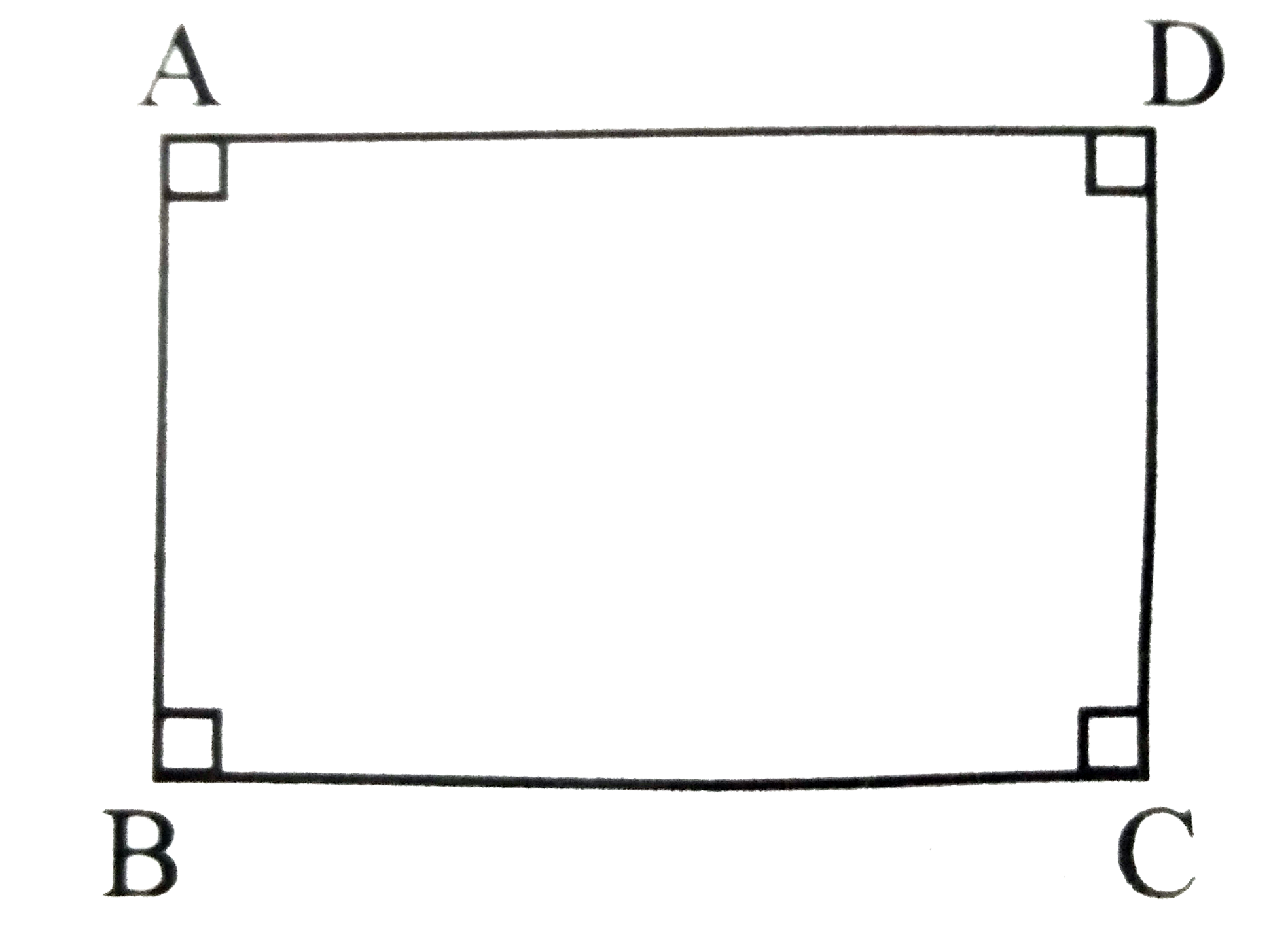
View SolutionProve that, any rectangle is a cyclic quadrilateral.
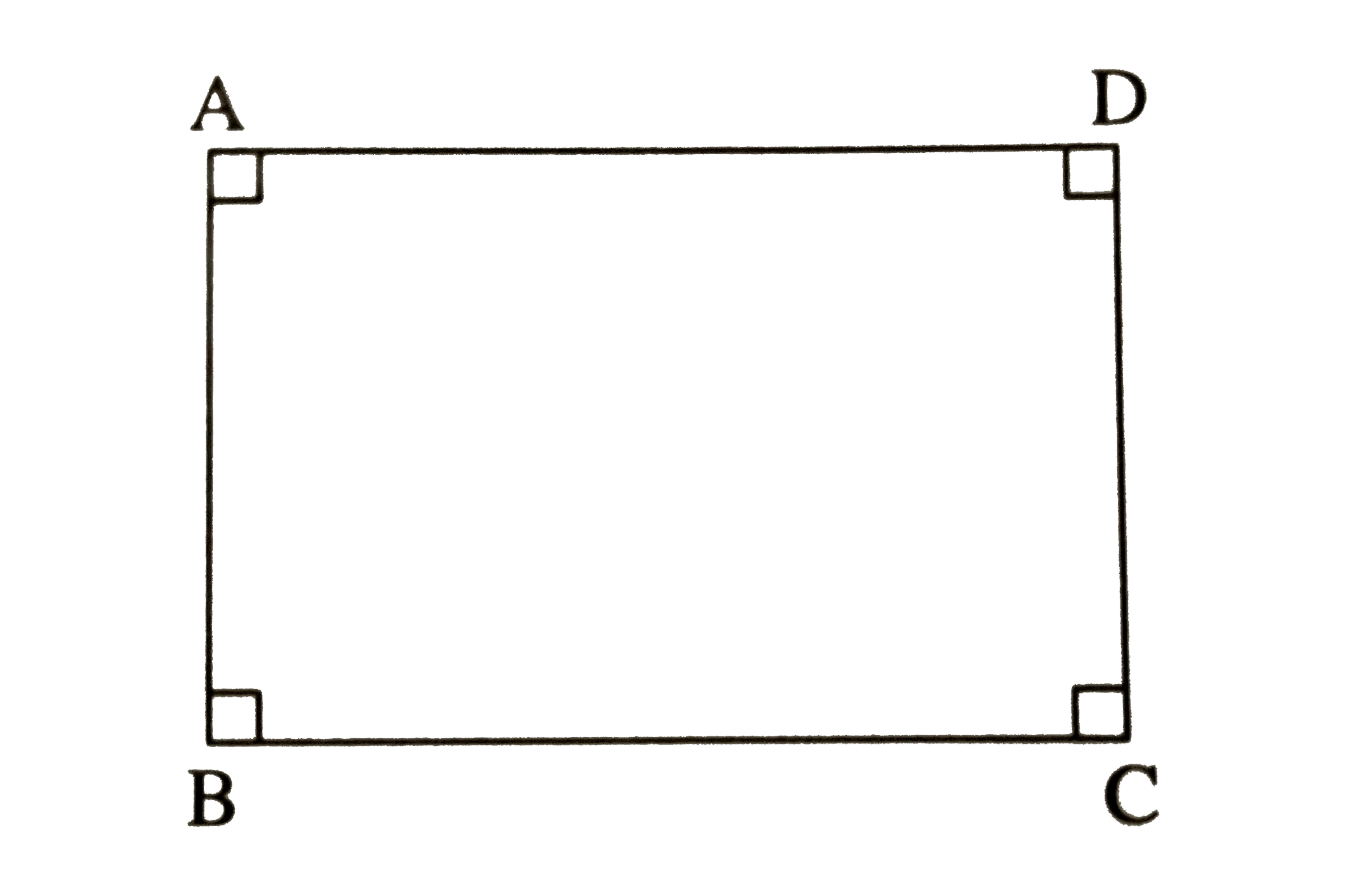
View Solution