Show that each diagonal of a parallelogram divide it into two congruent triangles.
The following are the steps involved in showing the above result. Arrange them in sequential order.
A) In $△ A B C$ and $△ C D A$ , AB=DC and BC=AD $(∴$ opposite angles of parallelogram) AC=AC (common side).
B) Let ABCD be a parallelogram. Join AC.
C) By SSS congruence property, $△ A B C ≅ △ C D A$ .
D) Similarly, BD divides the triangle into two congruent triangles.

A

BACD

B

BDAC

C

BADC

D

BDCA

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

BACD is the required sequential order.

|

Updated on:21/07/2023

Class 9 MATHS COORDINATE GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Prove that each of the following diagonals of a parallelogram divides it into two congurent triangles. The following lowing are the steps involved in proving the above results. Arrange them in sequential order.

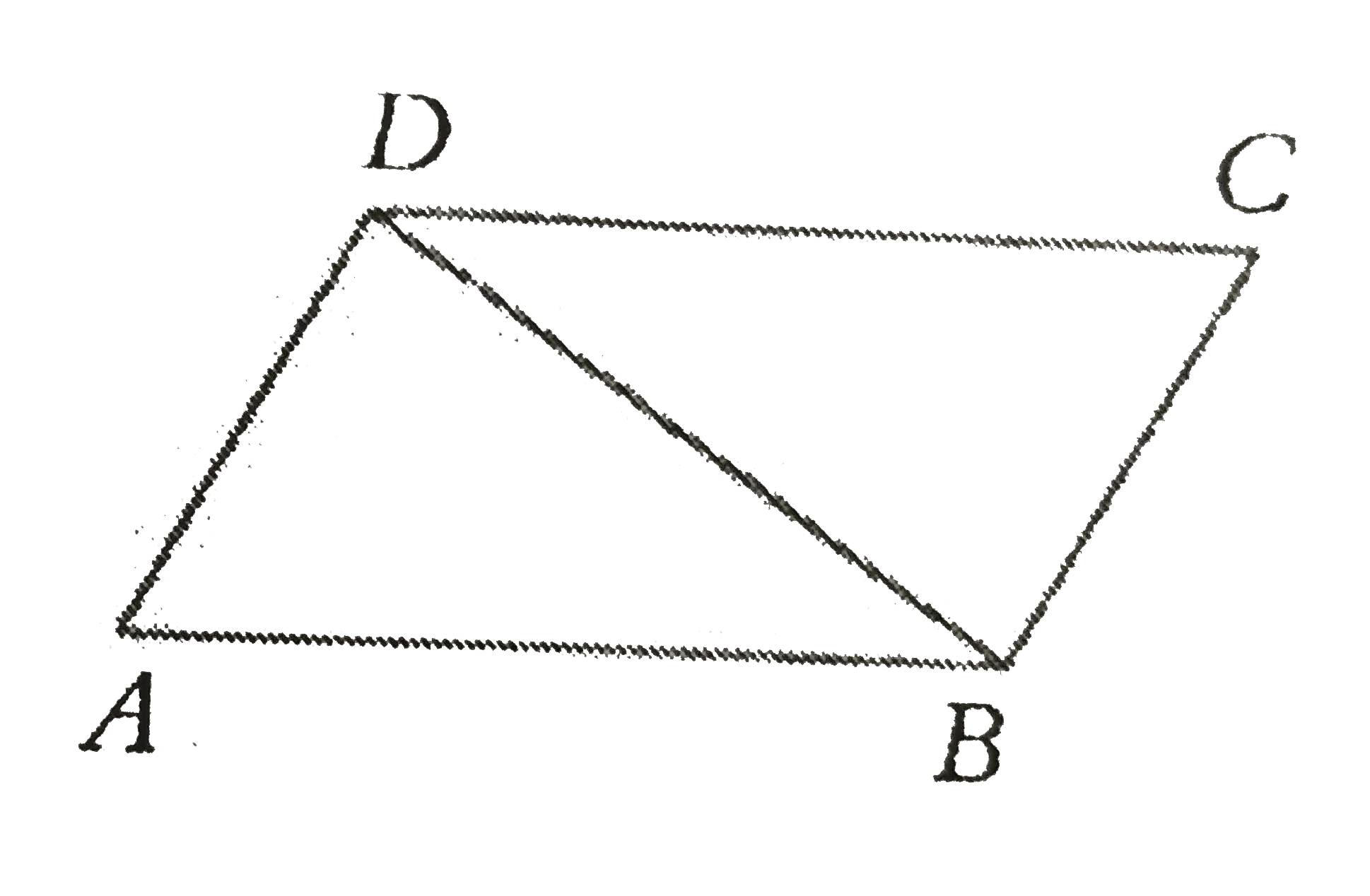
(A) By SSS conguruence property , $Δ D A B ≅ Δ B C D$ .
(B) Let ABCD be a parallelogram and join BD.
(C ) $A B = C D, A D = B C$ (opposite sides of parallelogram) and $B D = B D$ (common side).
(D ) Similarly , AC divides the parallelogram into two congruent triangles.
AABCD
BBCAD
CBACD
DCBAD
Question 2 - Select One
If ABCD is a parallelogram, then $- - \to A C - - - \to B D =$
A $4 - - \to A B$
B $3 - - \to A B$
C $2 - - \to A B$
D $- - \to A B$

PEARSON IIT JEE FOUNDATION-GEOMETRY-CONCEPT APPLICATION

Home
Ask Doubt
Profile