In the given figure, P,Q,R and S are concylic points, and O is the mid-point of the diameter QS. If ∠QPR=25∘, then find ∠SQR.
130∘
120∘
75∘
100∘
The correct Answer is:A
Given, ∠QPR=25∘.
Since, QS is the diameter, ∠QPS=90∘.
⇒∠SPR=90−25∘=65∘
∴∠SOR=2×65∘=130∘.
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - SHORT ANSWER TYPE QUESTIONS18videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Level 39videos
COORDINATE GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONSEXERCISE - level 310videos
LINEAR EQUATIONS AND INEQUATIONS
Similar Questions
In the following figure, △PQR is right-angled at R and S is the mid-point of hypotenuse PQ. If RS=25cm and PR=48cm, then find QR.
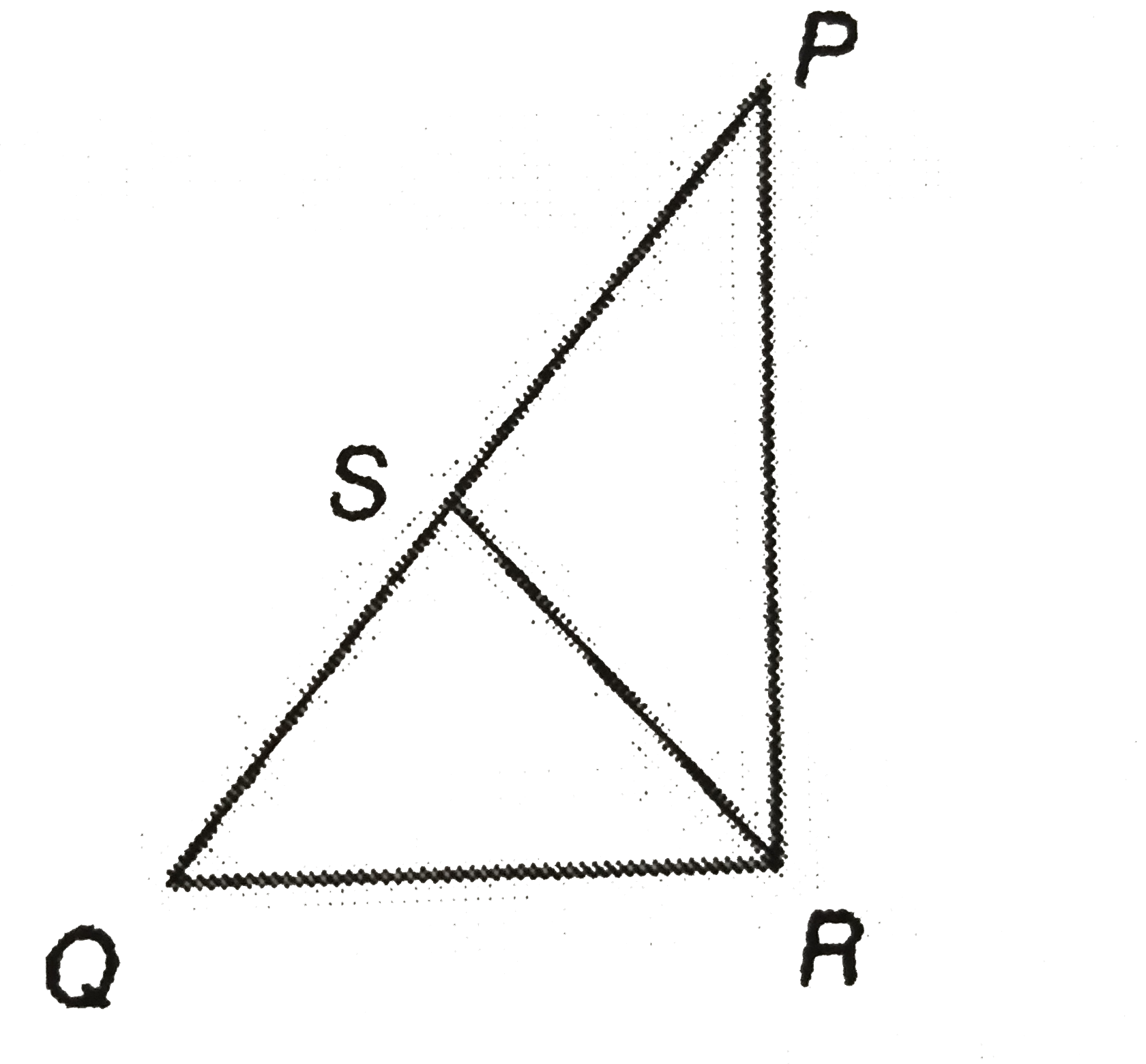
View Solution
In the figure above, KLMN is a rectangle . P,Q,R and S are the mid-points of ¯¯¯¯¯¯KL,¯¯¯¯¯¯¯LM,¯¯¯¯¯¯¯¯MN,and¯¯¯¯¯¯¯NK, respectively. If ∠KPS=30∘, then find ∠QRS.View SolutionIn the given figure, P (4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
View SolutionIn the given figure ∠PQR=100∘, where P,Q,R are points on a chords with centre O. Find the measure of ∠OPR.
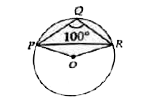
View SolutionIn the given figure, ∠PQR=100∘, where P, 9 and R are points on a circle with centre O. Find ∠OPR.
View Solution-
In the figure above, KLMN is a rectangle . P,Q,R and S are the mid-points of ¯¯¯¯¯¯KL,¯¯¯¯¯¯¯LM,¯¯¯¯¯¯¯¯MN,and¯¯¯¯¯¯¯NK, respectively. If ∠KPS=30∘, then find ∠QRS.View Solution In the given figure, PT is the tangent of a circle with centre O at point R. If diameter SQ is increased, it meets with PT at point P. If ∠SPR=x∘and∠QSR=y∘. What is the value of x∘+2y∘ ?
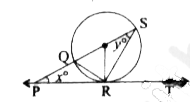
View SolutionIn the given figure, PQRS is a straight line R is the mid-point of QS and Q is the mid-point of PS. S is (6,5), R is (3, 5) and T is (4,8). Find the length of median TU. QRS
View SolutionIn the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of ΔBOEandΔABC
View SolutionIn the given figure, P is the mid-point of arc APB and M is the mid-int of chord AB of a circle with centre O. Prove that PM⊥AB
View Solution