In the given figure (not to scale), AC is the diameter of the circle and ∠ADB=20∘, then find ∠BPC.
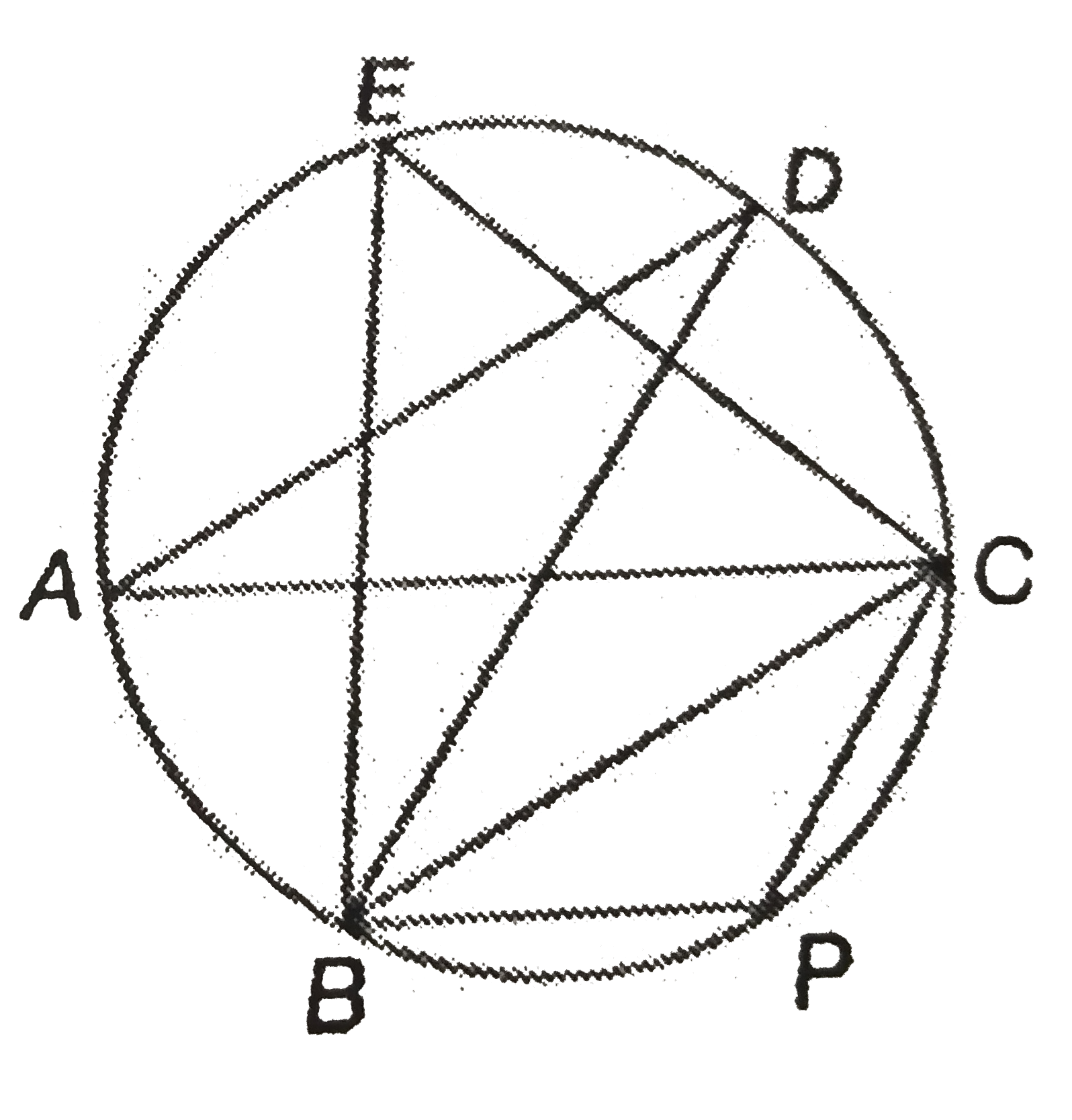
50∘
70∘
90∘
110∘
The correct Answer is:D
i) Join DC and use properties of cyclic quadrilateral.
ii) Use ∠ADC=90∘ and find ∠BDC.
iii) BDCP is cyclic.
Related Playlists
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - SHORT ANSWER TYPE QUESTIONS18videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Level 39videos
COORDINATE GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONSEXERCISE - level 310videos
LINEAR EQUATIONS AND INEQUATIONS
Similar Questions
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD:
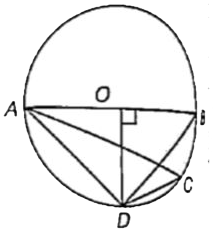 View Solution
View SolutionIn the given figure, ∠COB=40∘, AB is the diameter of the circle. Find ∠CAB :
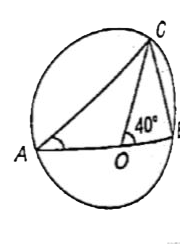 View Solution
View SolutionIn the given figure (not to scale), O is the center of the circle. If PB=PC, ∠PBO−25∘ and ∠BOC−130∘, then find ∠ABP+∠DCP.
 View Solution
View Solution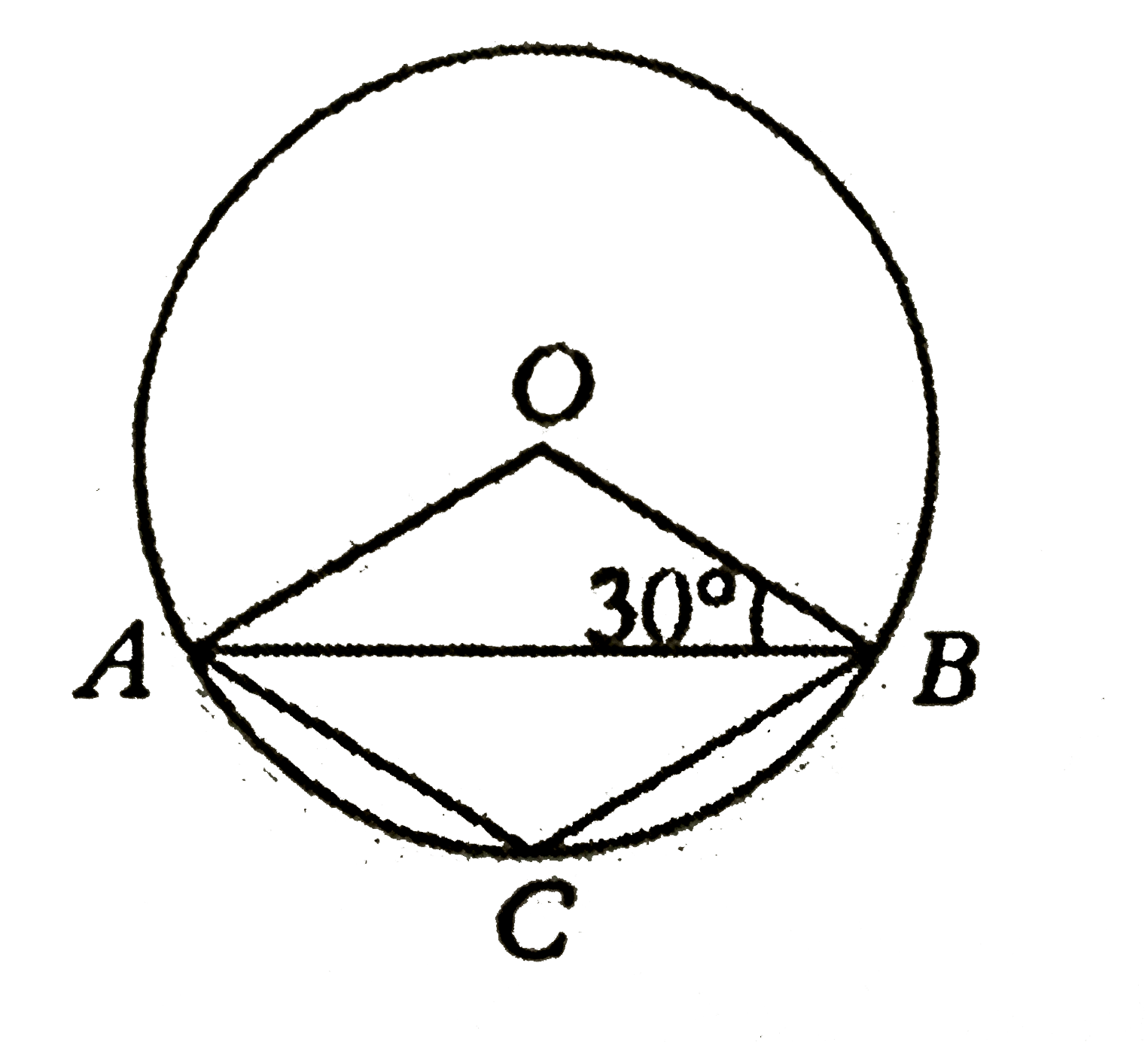
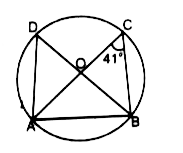
In the figure (not to scale ), O is the centre of the circle and ∠OBA=30∘. Find ∠ACBView SolutionIn the given figure, BD is the diameter of the circle and ∠BCA=41∘, then find the value of ∠ABD.
 View Solution
View Solution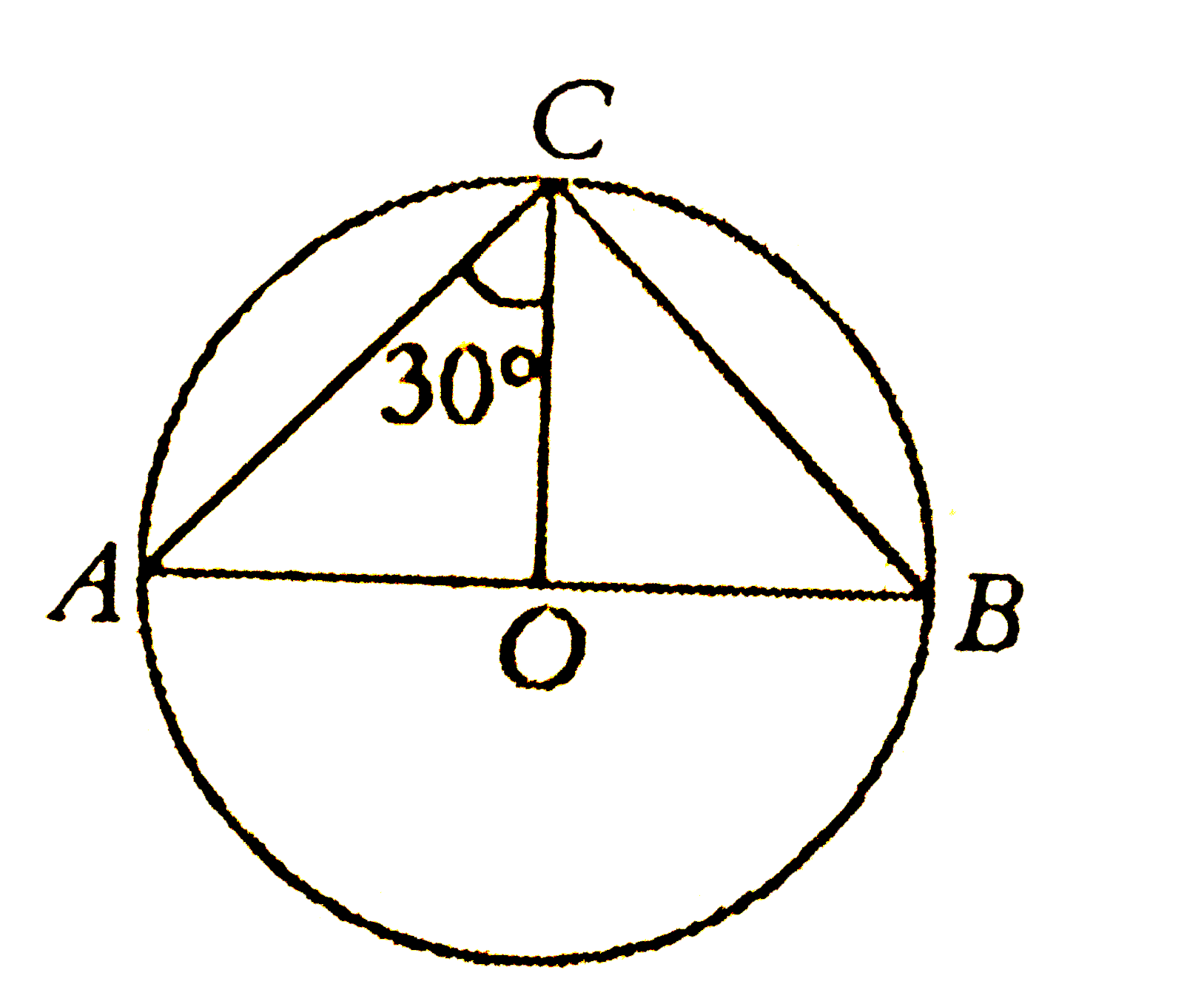
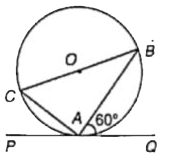
In the figure above (not to scale), AB is the diameter of the circle with centre O. If ∠ACO=30∘, then find ∠BOC.View SolutionIn the given figure, PAQ is the tangent. BC is the diameter of the circle. ∠BAQ=60∘, find ∠ABC :
 View Solution
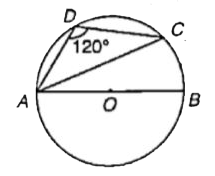
View SolutionIn the given figure, AB is the diameter of the circle, ∠ADC=120∘. Find ∠CAB:
 View Solution
View SolutionIn the given figure, ∠COB=40∘,AB is the diameter of the circle. Find m∠CAB:
 View Solution
View Solution
In the figure (not to scale ), O is the centre of the circle and ∠OBA=30∘. Find ∠ACBView Solution


