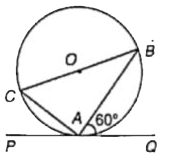
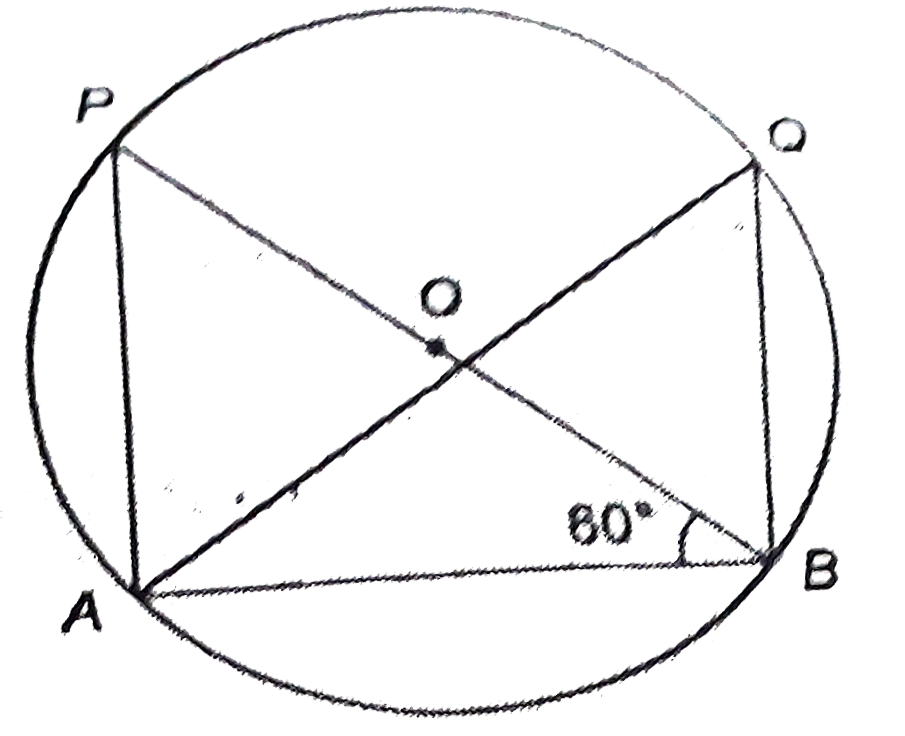
In the given figure, PAQ is the tangent. BC is the diameter of the circle. ∠BAQ=60∘, find ∠ABC :
A
25∘
B
30∘
C
45∘
D
60∘
Video Solution
Text Solution
The correct Answer is:B
|
Answer
Step by step video, text & image solution for In the given figure, PAQ is the tangent. BC is the diameter of the circle. angleBAQ = 60^(@), find angleABC : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 1)
54 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)
52 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.4
10 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
- HCF AND LCMBOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions
18 Videos
Similar Questions
Knowledge Check
In the given figure, PAQ is the tangent. BC is the diameter of the circle. ∠BAQ=60∘, find ∠ABC :
 A25∘B30∘C45∘D60∘
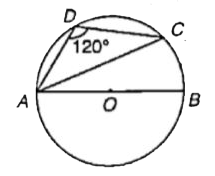
A25∘B30∘C45∘D60∘In the given figure, AB is the diameter of the circle, ∠ADC=120∘. Find ∠CAB:
 A20∘B30∘C40∘Dcan't be determined
A20∘B30∘C40∘Dcan't be determinedIn the given figure, AB is the diameter of the circle. Find the value of ∠ACD:
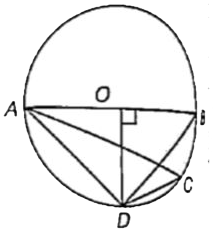 A30∘B60∘C45∘D25∘
A30∘B60∘C45∘D25∘
In the given figure, ∠COB=40∘, AB is the diameter of the circle. Find ∠CAB :
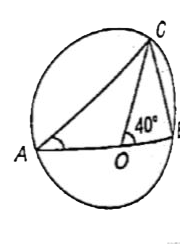
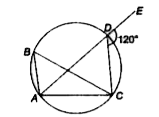
View SolutionIn the given figure, the value of ∠ABC is
View SolutionIn the adjoining figure, BP is the diameter of the circle. If ∠ABP=60∘, then find ∠AQB.
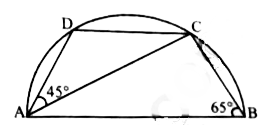
View SolutionIf the given figure, AB is diameter of the circle, C and D lie on the semicircle. ∠ABC=65∘and∠CAD=45∘, find ∠DCA.
View SolutionIn figure, BC is a diameter of the circle and ∠BAO=60∘. Then,∠ADCis equal to
View Solution