A bullet of mass m = 50 gm strikes a sand bag of mass M = 5 kg hanging from a fixed point, with a horizontal velocity →vp . If bullet sticks to the sand bag then the ratio of final & initial kinetic energy of the bullet is (approximately) :
Since the bullet strikes the sand bag with a horizontal velocity of magnitude vp. Therefore, its momentum just before the impact =p1=mVp.
Let the speed of the combination (sand bag + bullet) just after the impact be v.. Therefore the momentum of the system (sand bag + bullet) just after the impact =pf=(M+m)v.. Since no net horizontal external force acts on the system (M+m) during the collision, its net momentum remains conserved during the impact
⇒pi=pf
⇒mv=(M+m)v.
⇒v.=(mM+m)v. Since m<<M,v.=mvM ...(1)
Fraction of KE lost by the bullet during impact
η=12mv.212mv2=(v.v)2 ....(2)
Using (1) and (2), we obtain,
η=(mM)2=(1/205)2=10−4
Topper's Solved these Questions
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:SOLVED PROBLEMS (OBJECTIVE)
Explore 18 Videos
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:SOLVED PROBLEMS (OBJECTIVE) ASSERTION REASONING TYPE
Explore 1 Video
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:(NUMERICAL BASED QUESTIONS)
Explore 4 Videos
- AC CIRCUITSBook:FIITJEEChapter:AC CIRCUITSExercise:ASSERTION REASONING TYPE
Explore 1 Video
- CURRENT ELECTRICITYBook:FIITJEEChapter:CURRENT ELECTRICITYExercise:Comprehension -4
Explore 3 Videos
Similar Questions
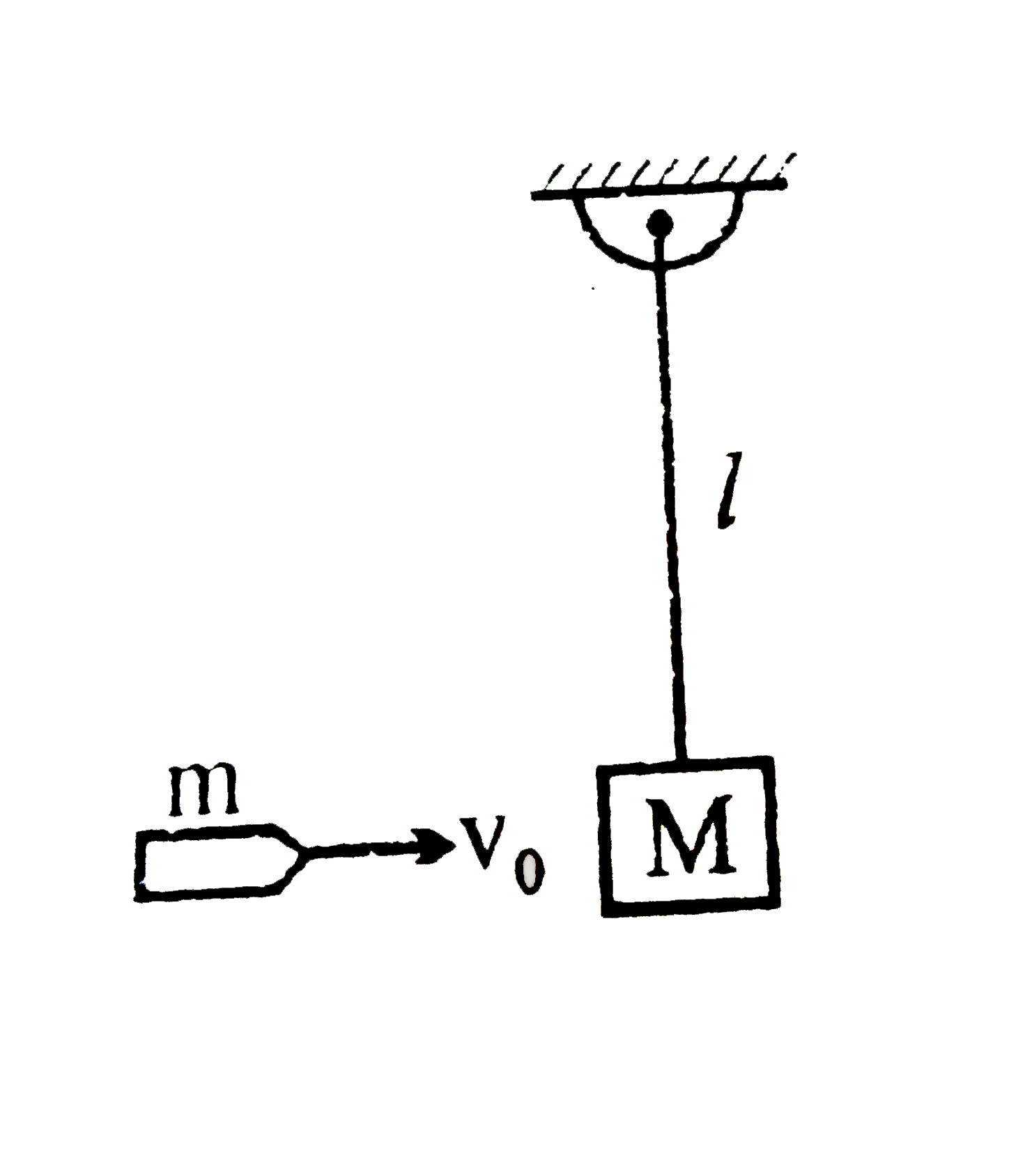
A bullet of mass m=10 gm strikes a hanging block of mass M=50 gm inelastically, with a horizontal velocity v0=60m/s. Find the change in tension (in N) in the string during collision. Round of to nearest integer. (Take : l=1m)
View SolutionA bullet of mass 5 g travels with a speed of 500m/s. If it penetrates a fixed target which offers a constant resistive force of 1000N to the motion of the bullet, find (a) the initial kinetic energy of the bullet (b) the distance through which the bullet has penetrated.
View Solution
Knowledge Check
A bullet of mass m=50 gm strikes (Δt≈0)a sand bag of mass M =5 kg hanging from a fixed point, with a horizontal velocity →vp. If bullet sticks to the sand bag then the ratio of final & initial kinetic energy of the bullet is
A10−2B10−3C10−6D10−4A bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
A√MM+nVB√mM+nVCmM+nVDV2A bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is
 A√2ghBM+mm√ghCmM+m2ghDM+mM√2gh
A√2ghBM+mm√ghCmM+m2ghDM+mM√2gh
A bullet of mass 50 g is fired from a gun with initial velocity of 35 m/s. If mass of the gun is 4 kg, then calculate the recoil velocity of the gun.
View SolutionA bullet of mass 50 g is fired from a gun with initial velocity of 35 m/s . If mass of the gun is 4 kg , then calculate the recoil velocity of the gun .
View SolutionA bullet of mass 10 g is fired from a gun of mass 1 kg with recoil velocity of gun 5 m/s. The muzzle velocity will be
View SolutionA bullet of mass 10gm strikes a target at 400m/s velocity and does half of its initial velocity. The loss of kinetic energy in joules is
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is

View Solution

