A bullet of mass m=10 gm strikes a hanging block of mass M=50 gm inelastically, with a horizontal velocity $v_{0} = 60 m / s$ . Find the change in tension (in N) in the string during collision. Round of to nearest integer. (Take : l=1m)

Video Solution

Text Solution

Verified by Experts

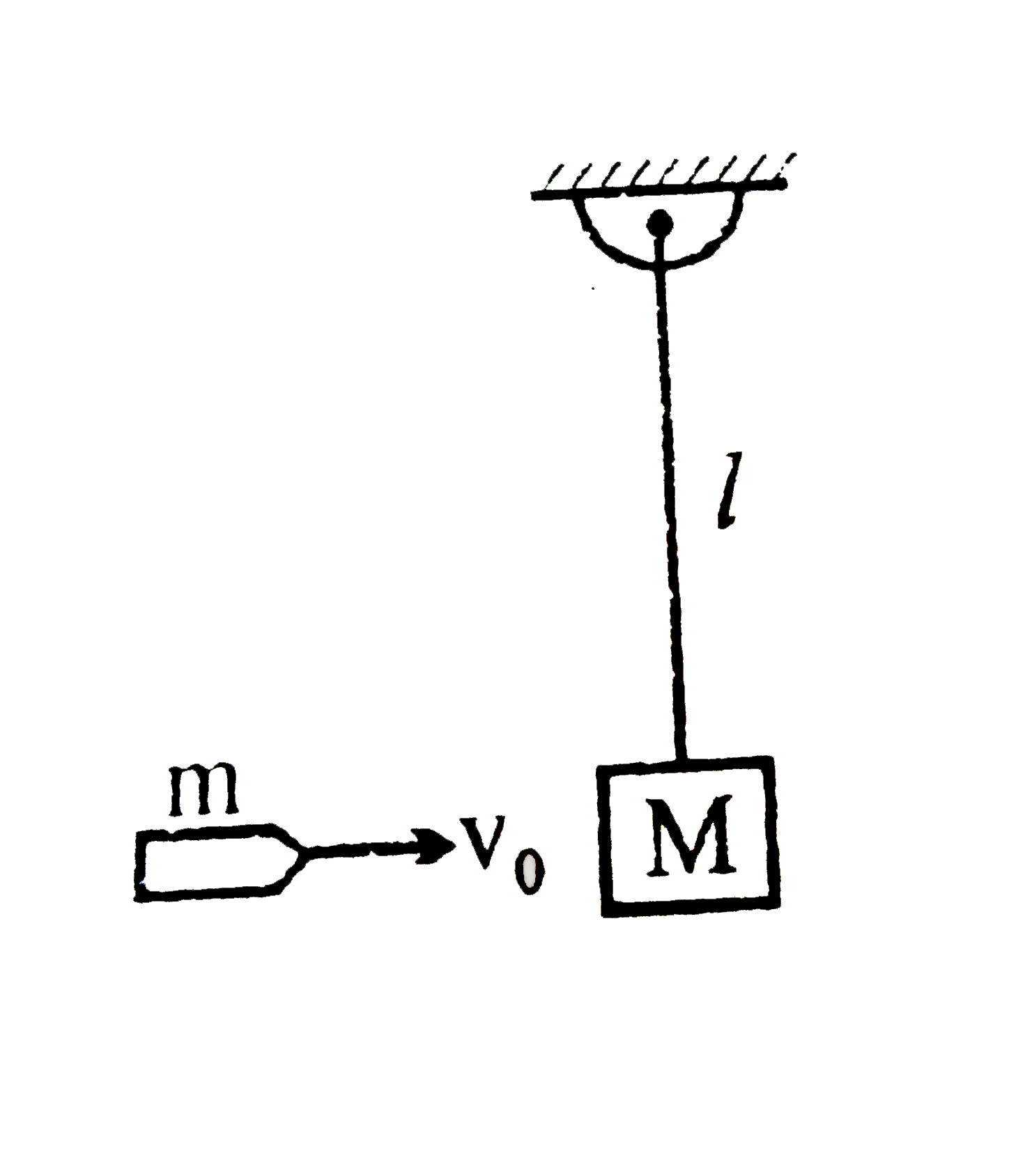
The correct Answer is:6

$T_{i} = M g$
$T_{f} - (M + m) g = (M + m) \frac{v^{2}}{l}$
$(M + m) v = m v_{0}$
$T_{f} = (M + m) g + (M + m) \frac{v_{0}^{2}}{{(M + m)}^{2} l} \times m^{2}$
$T_{f} - T_{i} = m g + \frac{m^{2} v_{0}^{2}}{(M + m) l}$
$= 0 \times 10^{- 1 / 3} \times 10 + \frac{10^{- 4} \times 3600}{60 \times 10^{- 3} \times 1} = 6.1 N$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A bullet of mass m = 50 gm strikes a sand bag of mass M = 5 kg hanging from a fixed point, with a horizontal velocity ${\to v}_{p}$ . If bullet sticks to the sand bag then the ratio of final & initial kinetic energy of the bullet is (approximately) :
A $10^{- 2}$
B $10^{- 3}$
C $10^{- 6}$
D $10^{- 4}$
Question 2 - Select One
A bullet of mass m=50 gm strikes $(Δ t \approx 0)$ a sand bag of mass M =5 kg hanging from a fixed point, with a horizontal velocity ${\to v}_{p}$ . If bullet sticks to the sand bag then the ratio of final & initial kinetic energy of the bullet is
A $10^{- 2}$
B $10^{- 3}$
C $10^{- 6}$
D $10^{- 4}$
Question 3 - Select One
A bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
A $\sqrt{\frac{M}{M + n}} V$
B $\sqrt{\frac{m}{M + n}} V$
C $\frac{m}{M + n} V$
D $\frac{V}{2}$

BANSAL-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile