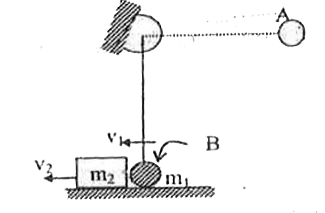
A steel ball of mass $0.5 k g$ is fastened to a cord $20 c m$ long and fixed at the far end and is released when the cord is horizontal. At the bottom of its path the ball strikes a $2.5 k g$ steel block initially at rest on a frictionless surface. The collision is elastic. The speed of the block just after the collision will be.

Video Solution

Text Solution

Verified by Experts

Let the ball strike the block with a speed $u_{1}$ . Since the initial speed (speed before collision) of the block $= u_{2} = 0$ for the perfectly elastic collision, the speed of the block is given as
$v_{2} = \frac{2 m_{1}}{m_{1} + m_{2}} u_{1} = \frac{2 \frac{m_{1}}{m_{2}}}{\frac{m_{1}}{m_{2}} + 1} u_{1}$
where $u_{1}$ can be found by conserving energy of the ball between the position A and B before collision of $m_{1}$ .
$\Rightarrow \frac{1}{2} m_{1} u_{1}^{2} - m_{1} g l = 0$
$\Rightarrow u_{1} = \sqrt{2 g l} = \sqrt{2 \times 10 \times 20} = 20$ m/sec.
$\frac{m_{1}}{m_{2}} = \frac{0.5 k g}{2.5 k g} = \frac{1}{5}$
By putting $u_{1} = 20$ m/sec and $\frac{m_{1}}{m_{2}} = \frac{1}{5}$ in (a) we obtain
$v_{2} = ⎧ ⎨ ⎩ \frac{2}{\frac{1}{5} + 1} ⎫ ⎬ ⎭ {\frac{1}{5}} (20) = \frac{20}{3} m / s$

Updated on:21/07/2023

A bullte weighing $5 g$ and moving with a velocity $600 m / s$ strikes a $5 k g$ block of ice resting on a frictionless surface. The speed of the block after the collision is
A $6 c m / s$
B $60 c m / s$
C $6 m / s$
D $0.6 c m / s$
A bullet weighing 10 gm and moving at 300 m/s strikes a 5 kg ice and drops dead. The ice block is placed on a frictionless level surface. The speed of the block after the collision, is
A6 cm/sec
B6 m/sec
C60 cm/sec
D60 m/sec
A ball of mass m suspended from a rigid support by an inextensible massless string is released from a height h above its lowest point. At its lowest point it collides elastically with a block of mass 2m at rest on a frictionless surface. Neglect the dimensions of the ball and the block. After the collision the ball rises to a maximum height of–

A $h / 3$
B $h / 2$
C $h / 8$
D $h / 9$