A man of mass m is standing on a stationary board of mass M kept on a fixed frictionless horizontal surface. The man starts running rightward on the board and acquires a speed u relative to the board. Find his speed relative to the fixed surface.
To solve the problem, we need to analyze the situation using the principle of conservation of momentum. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the system
We have a man of mass m standing on a board of mass M that is on a frictionless surface. Initially, both the man and the board are at rest.
Step 2: Define the velocities
Let:
- u be the speed of the man relative to the board when he starts running.
- V be the speed of the board relative to the ground.
- v be the speed of the man relative to the ground.
Step 3: Apply conservation of momentum
Since there are no external horizontal forces acting on the system, the momentum of the system must remain constant. Initially, the total momentum is zero (both the man and the board are at rest).
When the man runs to the right with speed u relative to the board, the board will move to the left to conserve momentum. Therefore, we can write the momentum conservation equation as:
m⋅v+M⋅V=0
Step 4: Relate the velocities
The speed of the man relative to the ground can be expressed as:
v=V+u
Step 5: Substitute v into the momentum equation
Substituting v into the momentum conservation equation gives us:
m(V+u)+MV=0
Step 6: Simplify the equation
Expanding the equation, we have:
mV+mu+MV=0
Combining the terms involving V:
(m+M)V+mu=0
Step 7: Solve for V
Rearranging the equation to solve for V:
(m+M)V=−mu
V=−mum+M
Step 8: Substitute back to find v
Now substituting V back into the equation for v:
v=V+u=−mum+M+u
Step 9: Combine the terms
To combine the terms, we can express v as:
v=u−mum+M
Step 10: Final expression
Thus, the final expression for the speed of the man relative to the fixed surface is:
v=u(1−mm+M)
This can be simplified further if needed, but this is the required speed of the man relative to the fixed surface.
We have a man of mass m standing on a board of mass M that is on a frictionless surface. Initially, both the man and the board are at rest.
Let:
- u be the speed of the man relative to the board when he starts running.
- V be the speed of the board relative to the ground.
- v be the speed of the man relative to the ground.
Since there are no external horizontal forces acting on the system, the momentum of the system must remain constant. Initially, the total momentum is zero (both the man and the board are at rest).
The speed of the man relative to the ground can be expressed as:
Substituting v into the momentum conservation equation gives us:
Expanding the equation, we have:
Rearranging the equation to solve for V:
Now substituting V back into the equation for v:
To combine the terms, we can express v as:
Thus, the final expression for the speed of the man relative to the fixed surface is:
Topper's Solved these Questions
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - SOLVED PROBLEMS (OBJECTIVE)
18 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - SOLVED PROBLEMS (OBJECTIVE) ASSERTION REASONING TYPE
1 Video
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - (NUMERICAL BASED QUESTIONS)
4 Videos
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSERTION REASONING TYPE
1 Video
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension -4
3 Videos
Similar Questions
A man of mass m1 is standing on a platform of mass m2 kept on a smooth horizontal surface. The man starts moving on the platform with a velocity vr relative to the platform. Find the recoil velocity of platform.
View SolutionA man of mass m1 = 80 kg is standing on a platform of mass m2 = 20 kg that lies on a frictionless horizontal surface. The man starts moving on the platform with a velocity vr = 10 m/s relative to the platform. Find the recoil speed of the platform.
View Solution
Knowledge Check
A man of mass m is standing on a stationary flat car of mass M. The car can move without friction along horizontal rails. The man starts walking with velocity v relative to the car. Work done by him
A(a) is greater than 12mv2 if he walks along rails.B(b) is less than 12mv2 is he walks along rails.C(c) is equal to 12mv2 is he walks normal to rails.D(d) can never be less than 12mv2A man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is
 A2uBu2CzeroDu4
A2uBu2CzeroDu4
A man of mass m is standing at one end of a trolley of mass M and length L placed at rest on a smooth horizontal surface. The man starts moving towards the other end and covers distance L, then distance moved by man w.r.t ground is
View SolutionA man of mass m1 is standing on a platform of mass m2 kept on a smooth horizontal surface. If the man moves a distance d w.r.t., the platform, find the displacement of the platform w.r.t., ground.
View SolutionNo external force: Stationery mass relative to an inertial frame remains at rest
A man of mass m is standing at one end of of a plank of mass M. The length of the plank is L and it rests on a frictionless horizontal ground. The man walks to the other end of the plank. Find displacement of the plank and man relative to the ground.

View SolutionA man of maas m is standing on a platform of maas M kept on smooth ice. If the man starts moving on the platform with a speed v relative to the platform with what velcity relative to the ice does the platform recoil?
View SolutionA 45.0kg girl is standing on plank that has a mass of 150kg. The plank, originally at rest, is free to slide on a frozen lake, which is a flat, frictionless supporting surface. The girl begins to walk alnong the plank at a constant speed of 1.50m/s relative to the plank. (a) What is her speed relative to the ice surface? (b) What is the speed of the plank relative to the ice surface?
View SolutionThe figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
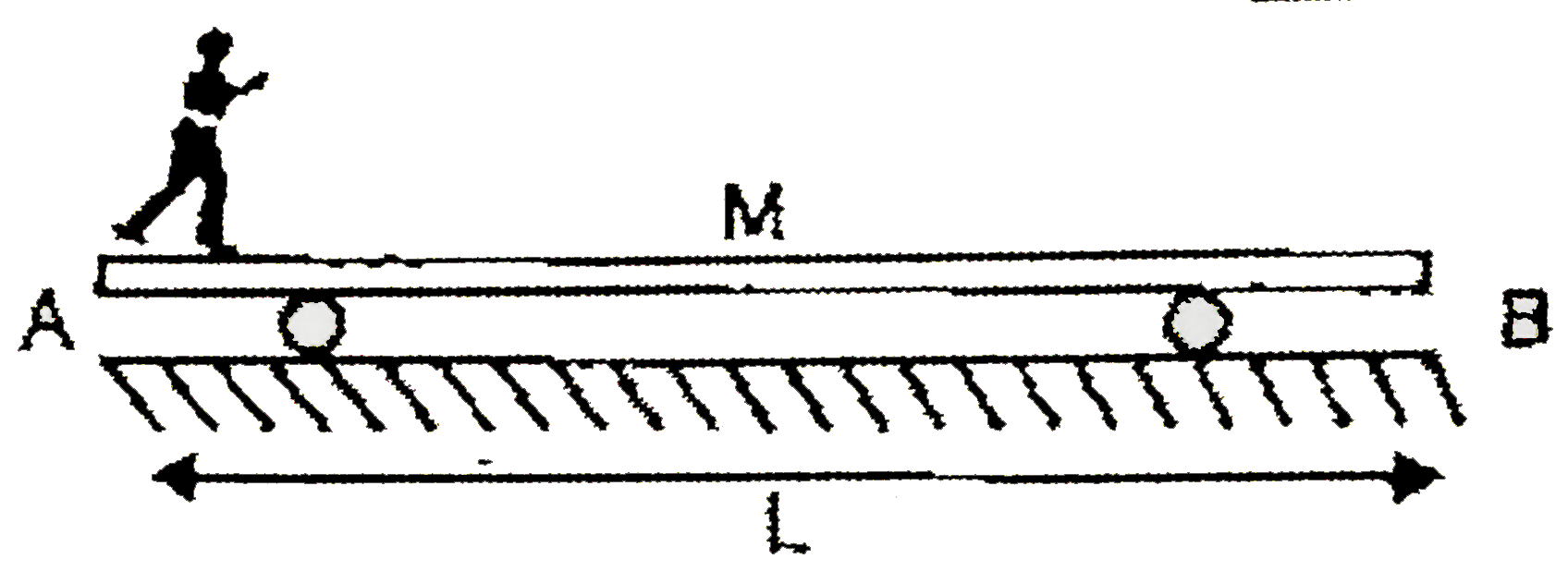
As the man walks on the trolley, the centre of mass of the system (man+ trolley) :
View Solution
