A man of mass m is standing at one end of a trolley of mass M and length L placed at rest on a smooth horizontal surface. The man starts moving towards the other end and covers distance L, then distance moved by man w.r.t ground is
mLM
ML/m
ml/m+M
ML/(m + M)
To solve the problem, we will use the principle of conservation of momentum and the concept of the center of mass.
1. Understanding the System:
- We have a man of mass m standing on a trolley of mass M and length L.
- Initially, both the man and the trolley are at rest on a smooth horizontal surface.
2. Movement of the Man:
- The man starts moving towards the other end of the trolley and covers a distance L relative to the trolley.
3. Defining Variables:
- Let x be the distance the trolley moves in the opposite direction while the man moves towards the other end.
- The distance the man moves with respect to the ground will be L−x.
4. Center of Mass Consideration:
- The center of mass of the system (man + trolley) must remain stationary since there are no external horizontal forces acting on the system.
- The position of the center of mass before and after the movement can be expressed as:
Initial center of mass=m⋅0+M⋅0m+M=0
- After the man moves, the center of mass position can be expressed as:
Final center of mass=m⋅(L−x)+M⋅xm+M
5. Setting the Center of Mass to Zero:
- Since the center of mass does not move, we set the final center of mass equal to zero:
m⋅(L−x)+M⋅xm+M=0
6. Solving for x:
- Multiply both sides by m+M:
m⋅(L−x)+M⋅x=0
- Rearranging gives:
mL−mx+Mx=0⟹mL=(m+M)x
- Solving for x:
x=mLm+M
7. Calculating the Distance Moved by the Man:
- The distance moved by the man with respect to the ground is:
Distance moved by man=L−x=L−mLm+M
- Simplifying this gives:
Distance moved by man=(m+M)L−mLm+M=MLm+M
Final Answer:
The distance moved by the man with respect to the ground is:
MLm+M
- We have a man of mass m standing on a trolley of mass M and length L.
- Initially, both the man and the trolley are at rest on a smooth horizontal surface.
- The man starts moving towards the other end of the trolley and covers a distance L relative to the trolley.
- Let x be the distance the trolley moves in the opposite direction while the man moves towards the other end.
- The distance the man moves with respect to the ground will be L−x.
- The center of mass of the system (man + trolley) must remain stationary since there are no external horizontal forces acting on the system.
- The position of the center of mass before and after the movement can be expressed as:
Initial center of mass=m⋅0+M⋅0m+M=0
- After the man moves, the center of mass position can be expressed as:
Final center of mass=m⋅(L−x)+M⋅xm+M
- Since the center of mass does not move, we set the final center of mass equal to zero:
m⋅(L−x)+M⋅xm+M=0
- Multiply both sides by m+M:
m⋅(L−x)+M⋅x=0
- Rearranging gives:
mL−mx+Mx=0⟹mL=(m+M)x
- Solving for x:
x=mLm+M
- The distance moved by the man with respect to the ground is:
Distance moved by man=L−x=L−mLm+M
- Simplifying this gives:
Distance moved by man=(m+M)L−mLm+M=MLm+M
The distance moved by the man with respect to the ground is:
MLm+M
Similar Questions
The figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.

When the man reaches the end B, the distance moves . by the trolley with respect to ground is:
View SolutionThe figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
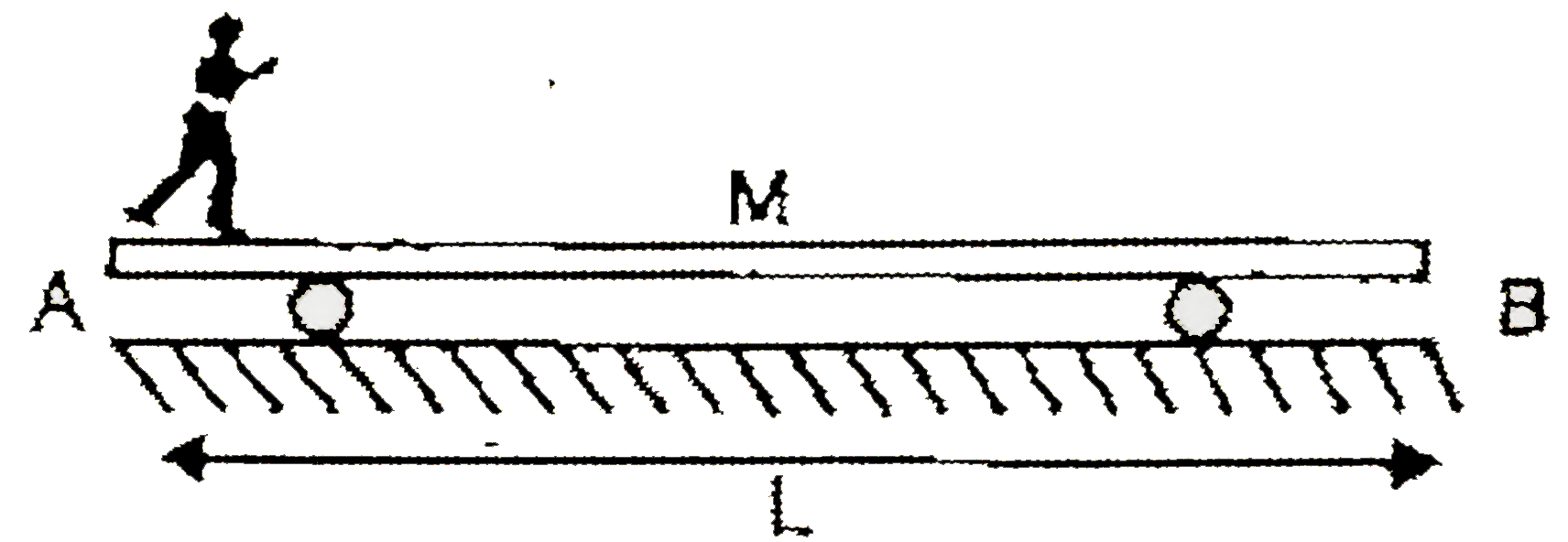
When the man starts moving, then the velocity of the trolley v2 with respect to ground will be:
View Solution
Knowledge Check
A boy of mass m is standing at one end of a boat of mass M and length l. The boy walks to the other end, the displacement of the
ACM is zeroBboat is mlM+mCboy is mlM+mDboat is mMlA man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is
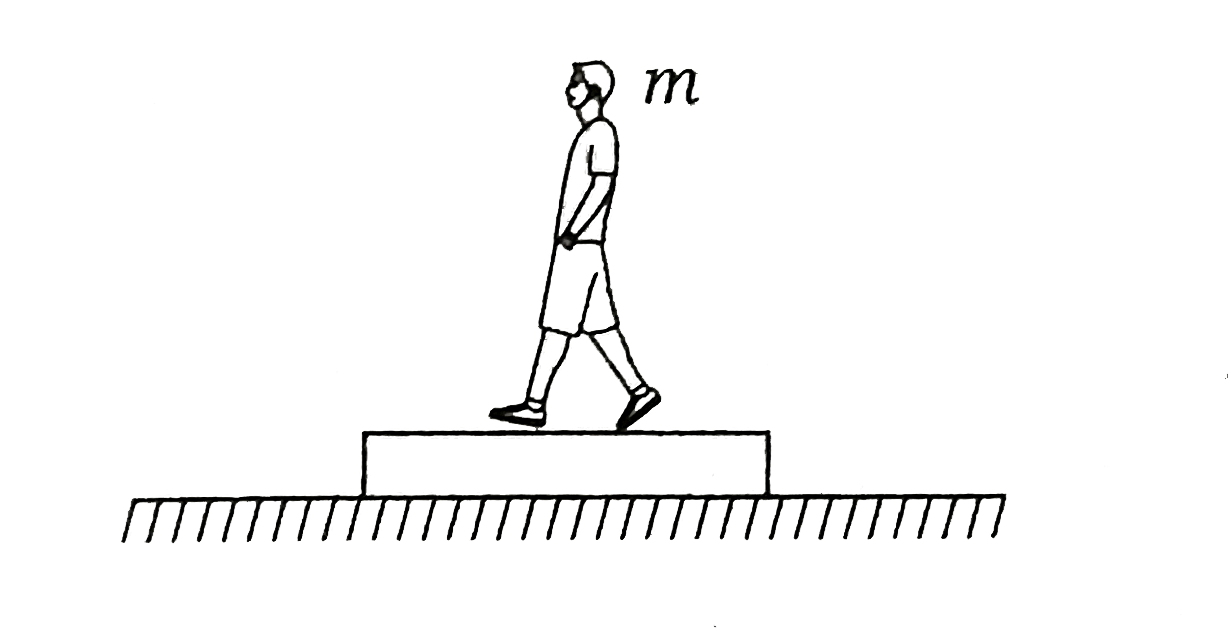 A2uBu2CzeroDu4
A2uBu2CzeroDu4
The figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
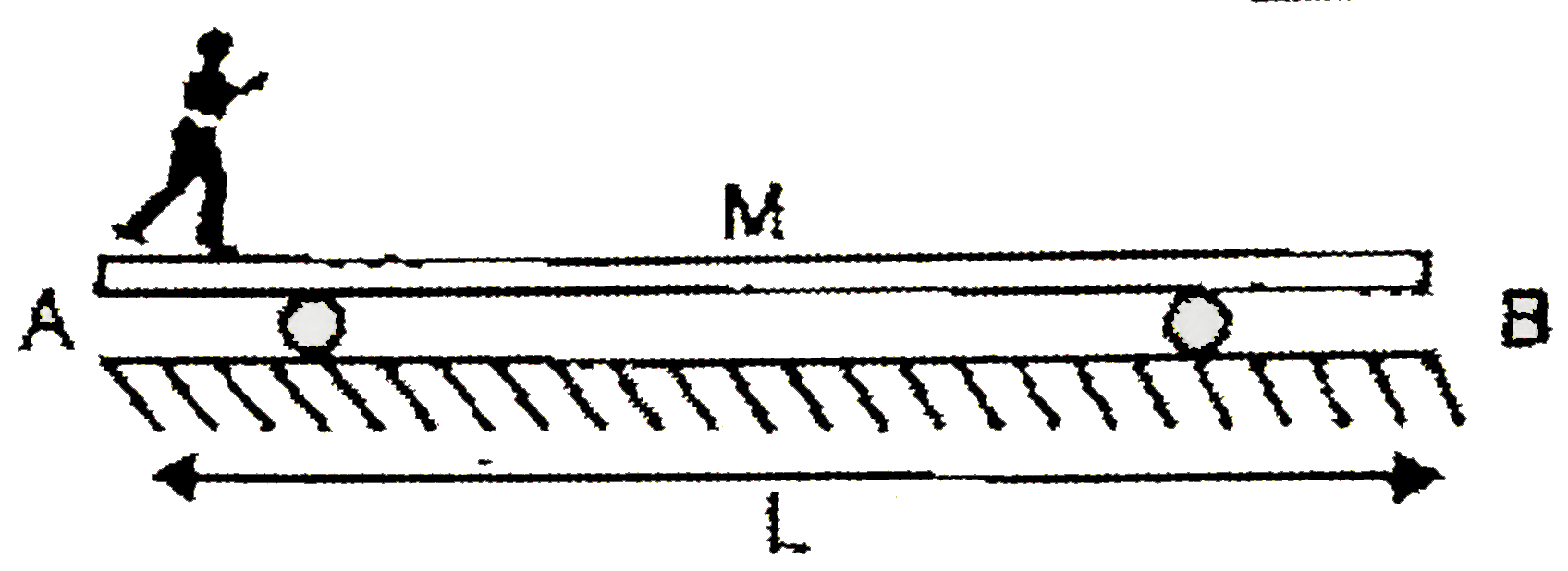
As the man walks on the trolley, the centre of mass of the system (man+ trolley) :
View SolutionThe figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
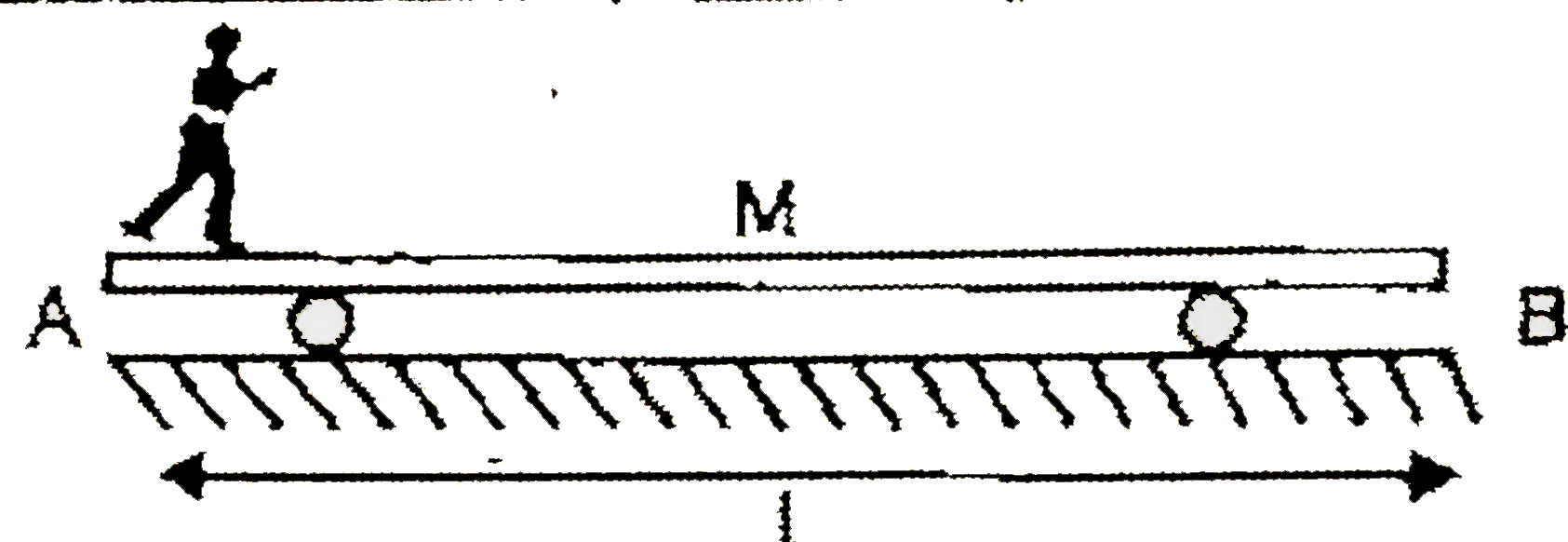
The time taken by the man to reach the other end is:
View SolutionThe figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
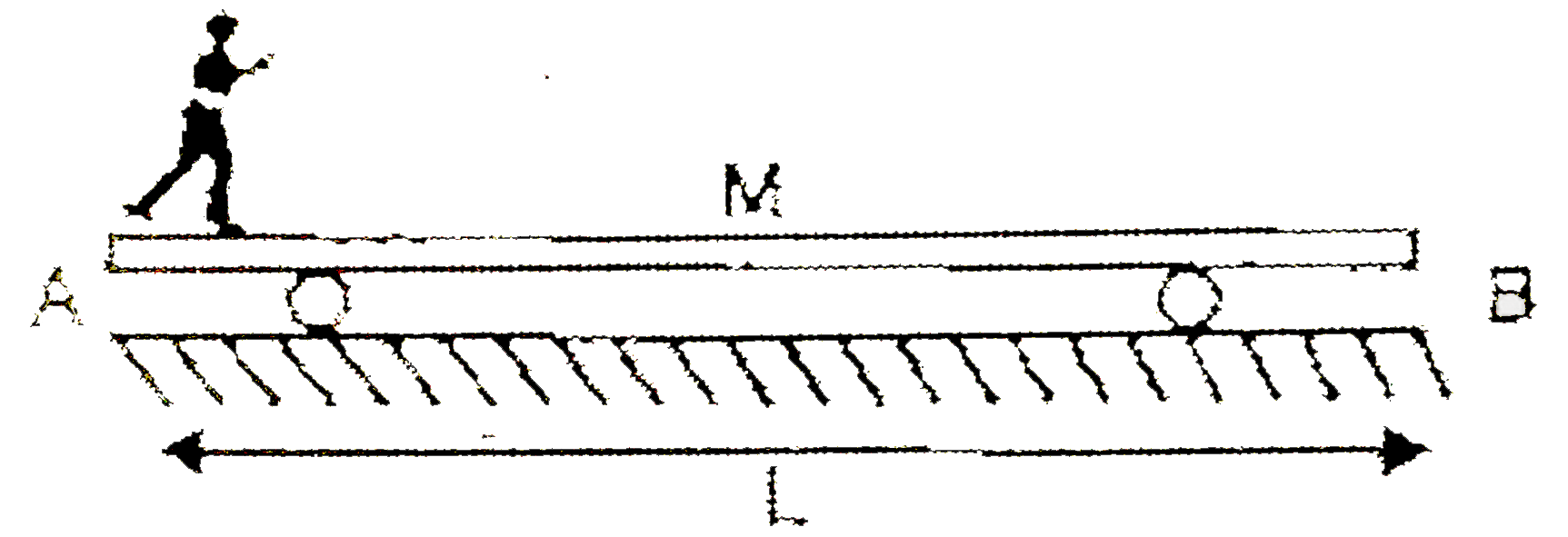
The velocity of the man with respect to ground v1 will be:
View SolutionThis figure shows a man of mass m standing at the end A to a trolley of mass M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.

(a) Find the time taken by the man to reach the other end.
(b) As the man walk on the trolley, find the velocity centre of mass of the system (man+trolley).
(c) When the man reaches the end B, find the distance moves by the trolley with respect to ground.
(d) Find the distance moved by the man with respect to ground.
View SolutionThe figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
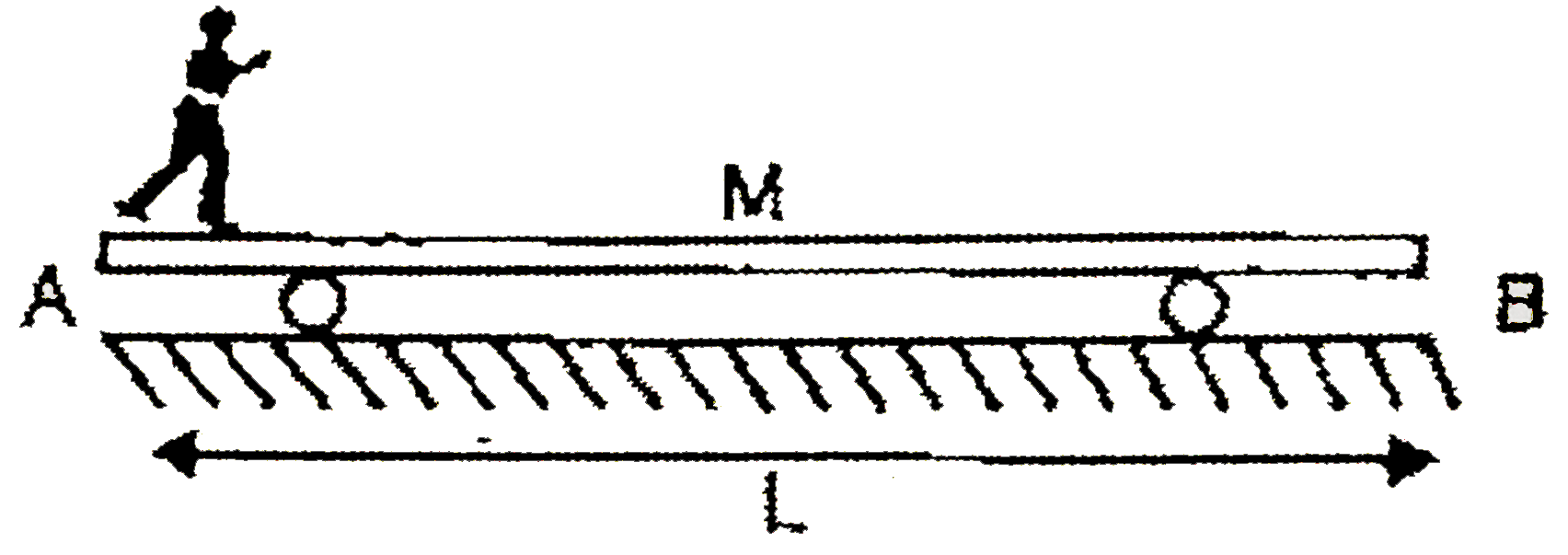
Choose the correct statement:
View SolutionNo external force: Stationery mass relative to an inertial frame remains at rest
A man of mass m is standing at one end of of a plank of mass M. The length of the plank is L and it rests on a frictionless horizontal ground. The man walks to the other end of the plank. Find displacement of the plank and man relative to the ground.

View Solution

