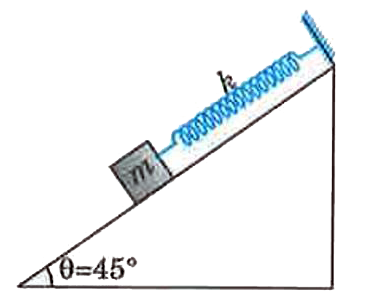
A spring of unstretched length 40 cm and spring constant k is attached to a block of mass 1 kg to one of its end. The other end of the spring is fixed on the top of a frictionless inclined plane of inclination θ=45∘ as shown in the figure, so that the spring extends by 3 cm. When the mass is displaced slightly and released the time period of the resulting oscillation is T. Determine the value of 5T close to nearest integer.
The correct Answer is:2

From the figure, we can say that the force which increases the length of the spring by x = 3 cm is F=mgsinθ. Therefore, the spring constant is
k=Fx=mgsinθx
Now time period T=2π√mk=2π√mk=2π√mmgsinθ/x
=2π√xgsinθ
Putting x=3cm=3×10−2m,g=9.8ms−2 and θ=45∘, we get
T=2π√xgsinθ=2π√3×10−29.8×sin45
=2π√3×10−29.8×0.707=0.4132s
Topper's Solved these Questions
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Competition ASSERTION REASON TYPE QUESTIONS
Explore 10 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Practice Test (For Board Examination)
Explore 12 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Competition File (MATRIX MATCH TYPE QUESTIONS)
Explore 2 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:CHAPTER PRACTICE TEST
Explore 16 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
Similar Questions
One end of a massless spring of relaxed length 50cm and spring constant k is fixed on top of a frictionless inclined plane of inclination theta=30degree as shown in fig. When a mass m=1.5kg is attached at the other end, the spring extends by 2.5cm when the block in equilibrium .The mass is displaced slightly from equilibrium position and released. The time period (in seconds) of the resulting oscillation will be (g=9.8m/s^(2))
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View Solution
Knowledge Check
A spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
Athe block will perform SHM of amplitude 5cmBthe block will have maximum velocity 30√5cm/sCthe block will have maximum acceleration 15m/s2Dthe minimum elastic potential energy of the spring will be zeroA block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be
 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3kmThree springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
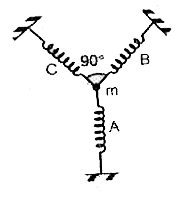 A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)
A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)

A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
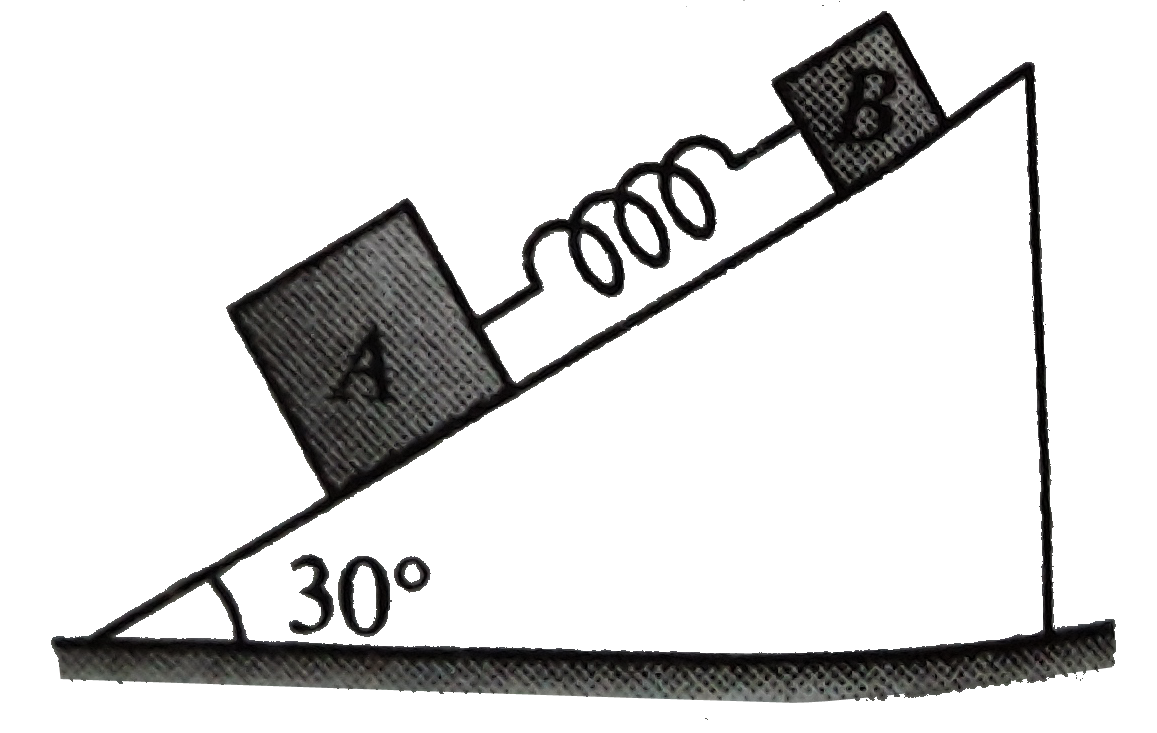
View SolutionTwo blocks A and B of masses 5kg and 2kg respectively connected by a spring of force constant =100Nm−1 are placed on an inclined plane of inclined 30∘ as shown in figure If the system is released from rest
View SolutionA particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
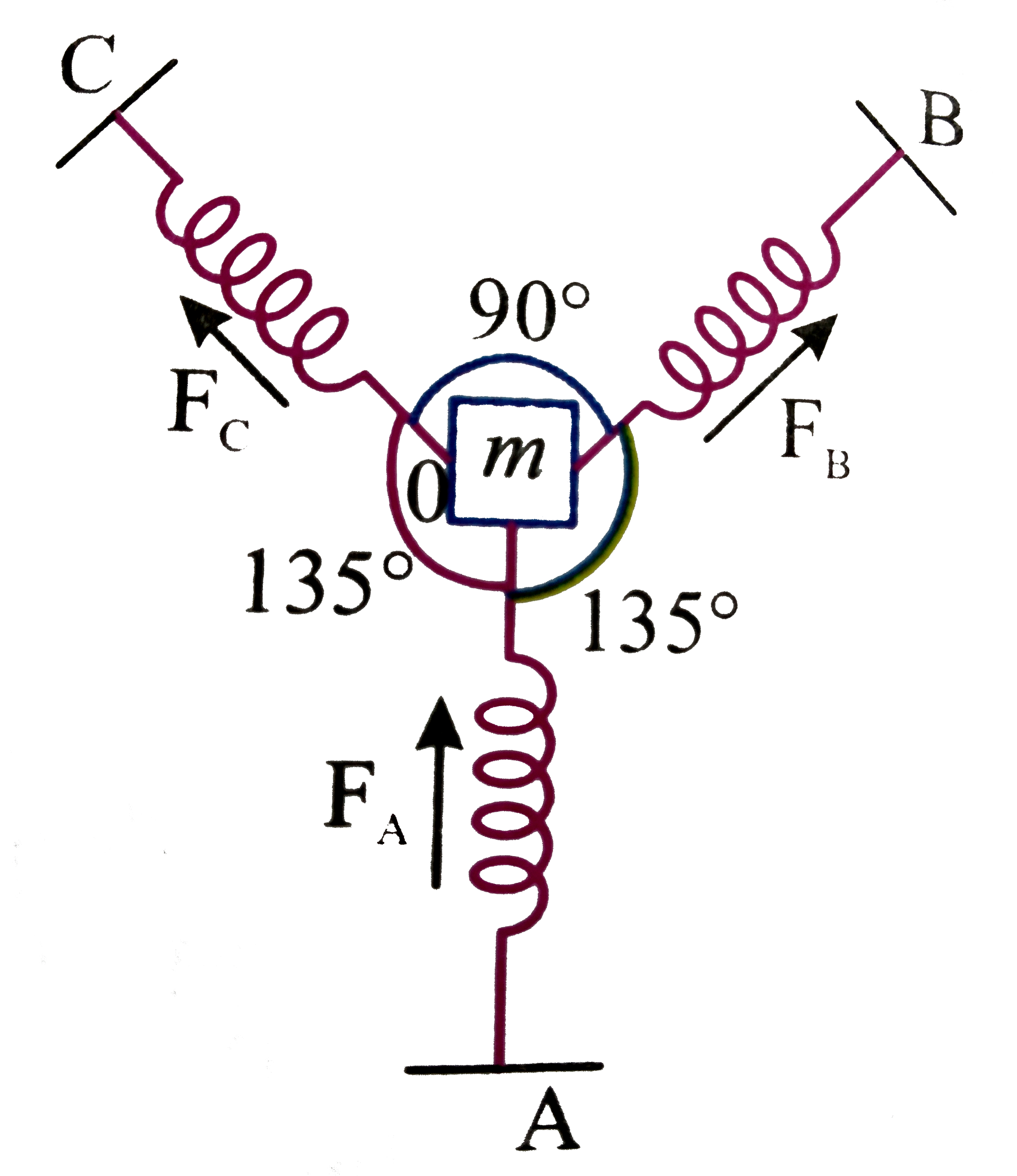
View SolutionSpring of spring constant k is attached with a block of mass m1, as shown in figure. Another block of mass m2 is placed angainst m1, and both mass masses lie on smooth incline plane.

Find the compression in the spring when lthe system is in equilibrium.
View SolutionA spring with one end attached to a mass and the other to a right support is stretched and released
View Solution