A mass of 0.2 kg, length 1m and cross sectional area 4.9×10−7m2 is suspended from a massless wire. The mass is pulled slightly in the vertically downward direction and released. It performs simple harmonic motion of angular frequency 70 rad s−1. If the Young's modulus of the material of the wire is x×109Nm−2, find the value of x.
The correct Answer is:2
To find the value of x in the Young's modulus of the material of the wire, we can follow these steps:
Step 1: Understand the relationship between Young's modulus, stress, and strain
Young's modulus Y is defined as the ratio of stress to strain:
Y=StressStrain
Step 2: Define stress and strain
Stress (σ) is given by:
σ=FA
where F is the force applied, and A is the cross-sectional area.
Strain (ϵ) is defined as:
ϵ=ΔLL
where ΔL is the change in length (extension) and L is the original length.
Step 3: Calculate the force acting on the wire
The force acting on the wire due to the suspended mass is the weight of the mass:
F=mg
where m=0.2kg and g≈9.81m/s2. Thus,
F=0.2×9.81=1.962N
Step 4: Substitute values into the stress formula
The cross-sectional area A is given as 4.9×10−7m2. Therefore, the stress is:
σ=FA=1.9624.9×10−7≈4.0×106N/m2
Step 5: Relate angular frequency to spring constant
The angular frequency ω of the simple harmonic motion is given as 70rad/s. The spring constant k can be related to ω and mass m by:
ω=√km⟹k=mω2
Substituting the values:
k=0.2×(70)2=0.2×4900=980N/m
Step 6: Calculate the strain
Using the relationship ΔL=mgk:
ΔL=1.962980≈0.002m
Now, the strain is:
ϵ=ΔLL=0.0021=0.002
Step 7: Substitute into Young's modulus formula
Now substituting stress and strain into the Young's modulus formula:
Y=σϵ=4.0×1060.002=2.0×109N/m2
Step 8: Find x
Given that Y=x×109N/m2, we can equate:
2.0×109=x×109
Thus, x=2.
Final Answer
The value of x is 2.
---
Young's modulus Y is defined as the ratio of stress to strain:
Y=StressStrain
Stress (σ) is given by:
σ=FA
where F is the force applied, and A is the cross-sectional area.
ϵ=ΔLL
where ΔL is the change in length (extension) and L is the original length.
The force acting on the wire due to the suspended mass is the weight of the mass:
F=mg
where m=0.2kg and g≈9.81m/s2. Thus,
F=0.2×9.81=1.962N
The cross-sectional area A is given as 4.9×10−7m2. Therefore, the stress is:
σ=FA=1.9624.9×10−7≈4.0×106N/m2
The angular frequency ω of the simple harmonic motion is given as 70rad/s. The spring constant k can be related to ω and mass m by:
ω=√km⟹k=mω2
Substituting the values:
k=0.2×(70)2=0.2×4900=980N/m
Using the relationship ΔL=mgk:
ΔL=1.962980≈0.002m
Now, the strain is:
ϵ=ΔLL=0.0021=0.002
Now substituting stress and strain into the Young's modulus formula:
Y=σϵ=4.0×1060.002=2.0×109N/m2
Given that Y=x×109N/m2, we can equate:
2.0×109=x×109
Thus, x=2.
The value of x is 2.
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition ASSERTION REASON TYPE QUESTIONS
10 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Practice Test (For Board Examination)
12 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (MATRIX MATCH TYPE QUESTIONS)
2 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
Assertion : For a particle excecuting simple harmonic motion , its velocity is maximum when the acceleration is minimum
Reason : In simple harmonic motion phase difference between displacement and velocity is (π2)
View SolutionAt which position the kinetic energy of a harmonic oscillator is maximum or minimum ?
View SolutionColumn I describes some situations in which a small object moves. Column II describes some characteristics of these motion. Match the situtions in column I with the characteristics in column II.

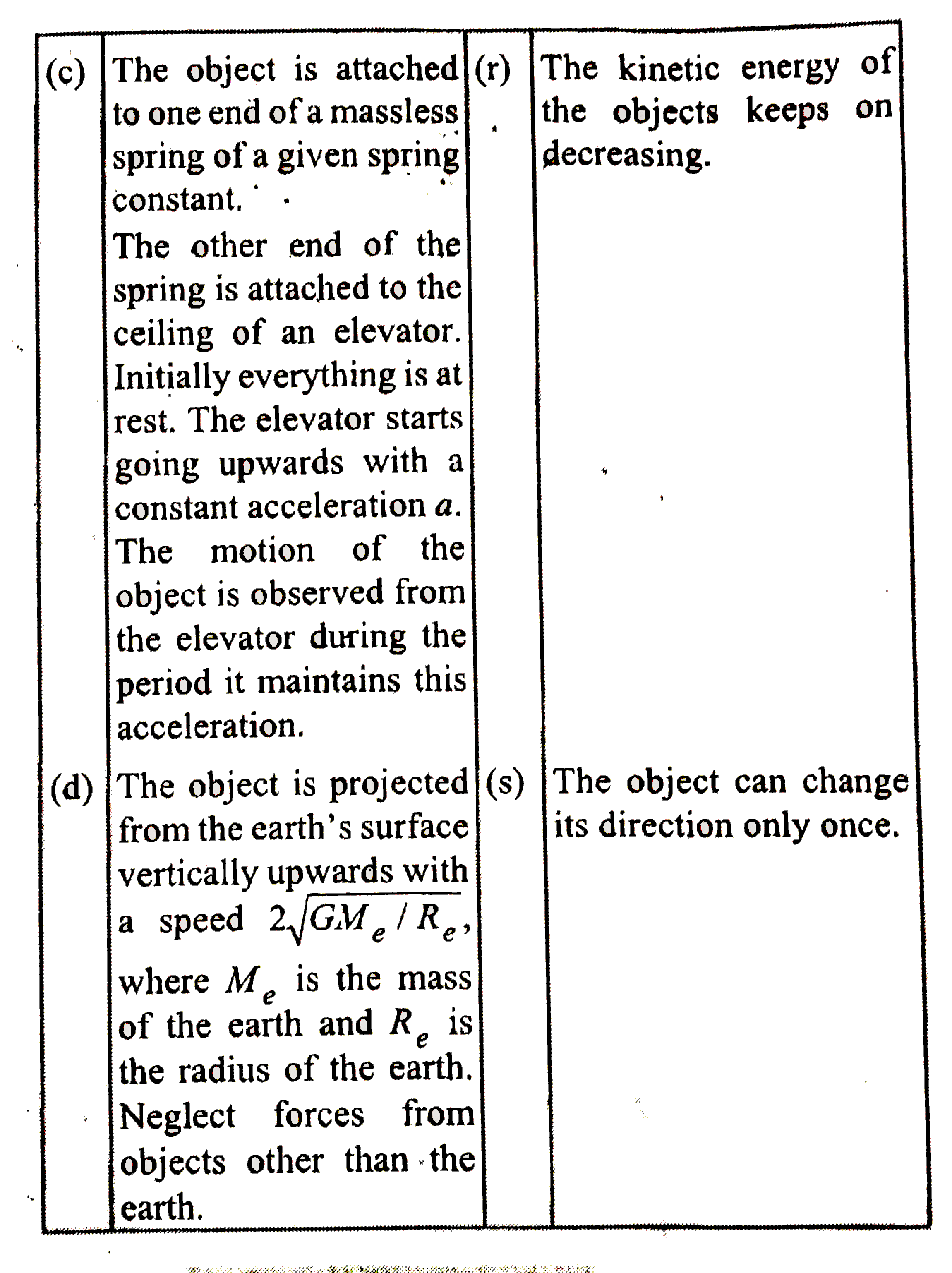
View SolutionWhen can say that circular motion is periodic ?
View SolutionWhat are the main features of gravitational force?
View SolutionA point mass m is suspended at the end of a massless wire of length l and cross section. If Y is the Young's modulus for the wire, obtain the frequency of oscillation for the simple harmonic motion along the vertical line.
View SolutionA 0.1kg mass is suspended from a wire of negligible mass. The length of the wire is 1m and its crosssectional are is 4.9xx10^-7m^2 . If the mass is pulled a little in the vertically downward direction and released, it performs simple harmonic motion of angular frequency 140 rad s^-1 . If the Young's modulus of the material of the wire is nxx10^9 Nm^-2 , the value of n is
View SolutionA 0.1kg mass is suspended from a wire of negligible mass. The length of the wire is 1m and its cross - sectional area is 4.9×10−7m2. If the mass is pulled a little in the vertically downward direction and released , it performs SHM with angular frequency 140rads−1. If the young's modulus of the material of the wire is p×109Nm−2, find the value of p.
View SolutionA copper wire of negligible mass, 1 m length and cross-sectional area 10^(6) m^(2) is kept on a smooth horizontal table with one end fixed. A ball of mass 1 kg is attached to the other end. The wire and the ball are rotating with an angular velocity of 20 rad//s . If the elongation in the wire is 10^(-3) m . a. Find the Young's modulus of the wire (in terms of xx 10^(11) N//m^(2) ). b. If for the same wire as stated above, the angular velocity is increased to 100 rad//s and the wire breaks down, find the breaking stress (in terms of xx 10^(10) N//m^(2) ).
View SolutionThe length of a wire is 1.0m and the area of cross-section is 1.0×10−2cm2. If the work done for increase in length by 0.2cm is 0.4 joule, then Young's modulus of the material of the wire is
View Solution0.1 kg का एक द्रव्यमान नगण्य द्रव्यमान वाले एक तार से लटका है। इस तार की लम्बाई 1m तथा इसके अनुप्रस्थ परिच्छेद का क्षेत्रफल 4.9×10−7 −2 है। यदि इस द्रव्यमान को थोड़ा-सा ऊर्ध्वाधर नीचे की ओर खींचकर छोड़ा जाये तो यह 140 rad s-1 कोणीय आवृत्ति की सरल आवर्त गति करता है। यदि तार के पदार्थ का यंग गुणांक n×109Nm−2 हो, तो n का मान है।
View SolutionAn object of mass m is suspended at the end of a massless wire of length L and area of cross -section A. Young modulus of the material of the wire is Y. If the mass is pulled down slightly its frequency of oscillation along the vertical direction is :
View SolutionA 0.1 kg mass is suspended from a wire of negligible mass. The length of the wire is 1 m and its cross sectional area is 4.9 times 10^-7 m^2 . IF the mass is pulled a little in the vertically downward direction and released, it performs simple harmonic motion of angular frequency 140 rad.s^-1 . If the young's modulus of the material of the wire is n times 10^9 N.m^-2 Calculate the value of n.
View SolutionA 0.1 kg mass is suspended from a wire of negligible mass. The length of the wire is 1 m and its cross sectional area is 4.9 times 10^-7 m^2 . IF the mass is pulled a little in the vertically downward direction and released, it performs simple harmonic motion of angular frequency 140 rad.s^-1 . IF the young's modulus of the material of the wire is n times 10^9 N.m^-2 . Find the value of n.
View SolutionA 0.1 kg mass is suspended from a wire of negligible mass. The length of the wire is 1m and its cross-sectional area is 4.9×10−7m2. If the mass is pulled a little in the vertically downward direction and released, it performs simple harmonic motion of angular frequency 140rad/s. If the Young's modulus of the material of the wire is n×109N⋅m−2, then find out the value of n.
View Solution
