The maximum seperation between two particles executing simple harmonic motion of the equal amplitude and same frequency along the same straight line and about the same mean position, is √3 times the amplitude of oscillation. IF the phase difference between them is ϕ, determine 2π/ϕ.
The correct Answer is:3
To solve the problem, we need to determine the phase difference ϕ between two particles executing simple harmonic motion (SHM) given that their maximum separation is √3 times the amplitude A.
1. Understanding the Motion:
- Let the displacements of the two particles be represented as:
x1=Asin(ωt)
x2=Asin(ωt+ϕ)
- Here, A is the amplitude, ω is the angular frequency, and ϕ is the phase difference between the two particles.
2. Finding the Separation:
- The separation x between the two particles is given by:
x=x2−x1=Asin(ωt+ϕ)−Asin(ωt)
- Using the sine subtraction formula, we can express this as:
x=A(sin(ωt+ϕ)−sin(ωt))
3. Using the Sine Difference Formula:
- The difference of sines can be expressed as:
sin(A)−sin(B)=2cos(A+B2)sin(A−B2)
- Applying this to our equation:
x=A⋅2cos(2ωt+ϕ2)sin(ϕ2)
- Thus, the maximum separation occurs when cos(2ωt+ϕ2)=1:
xmax=2Asin(ϕ2)
4. Setting Up the Equation:
- According to the problem, the maximum separation is given as:
xmax=√3A
- Therefore, we equate the two expressions:
2Asin(ϕ2)=√3A
- Dividing both sides by A (assuming A≠0):
2sin(ϕ2)=√3
5. Solving for sin(ϕ2):
- Rearranging gives:
sin(ϕ2)=√32
- The angle whose sine is √32 is:
ϕ2=π3(or 60∘)
6. Finding ϕ:
- Multiplying both sides by 2:
ϕ=2π3
7. Calculating 2πϕ:
- Finally, we compute:
2πϕ=2π2π3=3
Final Answer:
2πϕ=3
- Let the displacements of the two particles be represented as:
x1=Asin(ωt)
x2=Asin(ωt+ϕ)
- Here, A is the amplitude, ω is the angular frequency, and ϕ is the phase difference between the two particles.
- The separation x between the two particles is given by:
x=x2−x1=Asin(ωt+ϕ)−Asin(ωt)
- Using the sine subtraction formula, we can express this as:
x=A(sin(ωt+ϕ)−sin(ωt))
- The difference of sines can be expressed as:
sin(A)−sin(B)=2cos(A+B2)sin(A−B2)
- Applying this to our equation:
x=A⋅2cos(2ωt+ϕ2)sin(ϕ2)
- Thus, the maximum separation occurs when cos(2ωt+ϕ2)=1:
xmax=2Asin(ϕ2)
- According to the problem, the maximum separation is given as:
xmax=√3A
- Therefore, we equate the two expressions:
2Asin(ϕ2)=√3A
- Dividing both sides by A (assuming A≠0):
2sin(ϕ2)=√3
- Rearranging gives:
sin(ϕ2)=√32
- The angle whose sine is √32 is:
ϕ2=π3(or 60∘)
- Multiplying both sides by 2:
ϕ=2π3
- Finally, we compute:
2πϕ=2π2π3=3
2πϕ=3
Topper's Solved these Questions
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Competition ASSERTION REASON TYPE QUESTIONS
Explore 10 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Practice Test (For Board Examination)
Explore 12 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Competition File (MATRIX MATCH TYPE QUESTIONS)
Explore 2 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:CHAPTER PRACTICE TEST
Explore 16 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
Similar Questions
Two particles are in SHM with the same amplitude and frequency along the same line and about the same point. If the maximum separation between them is √3 times their amplitude, what is the phase difference between them?
View SolutionTwo particles are in SHM with the same amplitude and frequency along the same line and about the same point. If the maximum separation between them is √3 times their amplitude, the phase difference between them is 2πn. Find value of n
View Solution
Knowledge Check
A particle is subjected to two simple harmonic motions in the same direction having equal amplitudes and equal frequency. If the resulting amplitude is equal to the amplitude of individual motions, the phase difference between them is
Aπ3B2π3Cπ)6Dπ2Two particles execute simple harmonic motion of the same amplitude and frequency along close parallel lines. They pass each other moving in opposite directions each time their displacement is half their amplitude. Their phase difference is
A5π6B4π3Cπ6D2π3Two particles executes S.H.M. of the same amplitude and frequency along the same straight line. They pass one another when going in opposite directions, each time their displacement is root three by two times amplitude. The phase difference between them is
A2π3 radBπ2 radCπ6 radDπ3 rad
Find the phase different between two particles executing simple harmonic motion with the same amplitude and frequency when their phases at a certain moment are as shown in the figure.
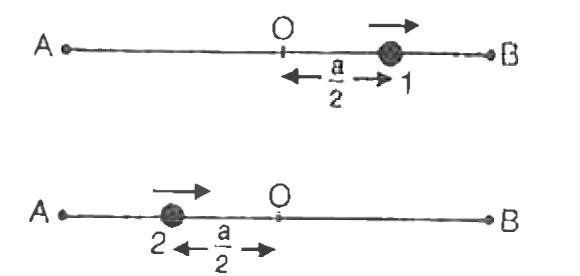
View SolutionA particle is subjected to two simple harmonic motions in the same direction having equal amplitude and equal frequency. If the resultant amplitude is equal to the amplitude of individual motions, what is the phase difference between the motions.
View SolutionA particle is subjected to two simple harmonic motion in the same direction having equal amplitudes and equal frequency. If the resultant amplitude is equal to the amplitude of the individual motions. Find the phase difference between the individual motions.
View SolutionFind the phase difference between two particles executing simple harmonic motion with the same frequency if they are found inn the states shown in the figures at four different points of time.
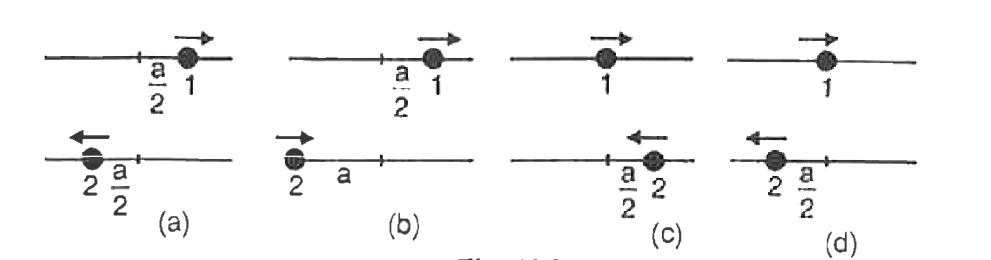
View SolutionTwo particles P and Q performs S.H.M. of same amplitude 'A' and frequency n along the same straight line the resultant S.H.M. have the amplitude √2 times amplitude of individual. The initial phase difference between two particles will be nearly.
View Solution

