If AD is the internal angle bisector of with AB = 3 cm and AC = 1 cm, then what is BD : BC equla to ?
The correct Answer is:D
To solve the problem, we will use the Angle Bisector Theorem, which states that the ratio of the lengths of the two segments created by the angle bisector on the opposite side is equal to the ratio of the lengths of the other two sides of the triangle.
1. Identify the Given Information:
- We have triangle ABC with sides AB = 3 cm and AC = 1 cm.
- AD is the internal angle bisector of angle A.
2. Apply the Angle Bisector Theorem:
According to the Angle Bisector Theorem:
ABAC=BDDC
Here, AB = 3 cm and AC = 1 cm.
3. Set Up the Ratio:
Substitute the values into the equation:
31=BDDC
This implies:
BD=3⋅DC
4. Express BC in Terms of BD and DC:
The total length of BC can be expressed as:
BC=BD+DC
5. Substitute BD in Terms of DC:
From the previous step, we know:
BD=3⋅DC
Therefore, substituting this into the equation for BC:
BC=3⋅DC+DC=4⋅DC
6. Find the Ratio of BD to BC:
Now we can find the ratio of BD to BC:
BDBC=3⋅DC4⋅DC
The DC cancels out:
BDBC=34
7. Final Answer:
Therefore, the ratio BD:BC is:
3:4
- We have triangle ABC with sides AB = 3 cm and AC = 1 cm.
- AD is the internal angle bisector of angle A.
According to the Angle Bisector Theorem:
ABAC=BDDC
Here, AB = 3 cm and AC = 1 cm.
Substitute the values into the equation:
31=BDDC
This implies:
BD=3⋅DC
The total length of BC can be expressed as:
BC=BD+DC
From the previous step, we know:
BD=3⋅DC
Therefore, substituting this into the equation for BC:
BC=3⋅DC+DC=4⋅DC
Now we can find the ratio of BD to BC:
BDBC=3⋅DC4⋅DC
The DC cancels out:
BDBC=34
Therefore, the ratio BD:BC is:
3:4
Topper's Solved these Questions
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.1
Explore 45 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.2
Explore 100 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:EXERCISE(LEVEL 2)
Explore 52 Videos
- FUNDAMENTALS Book:ARIHANT SSCChapter:FUNDAMENTALS Exercise:TEST OF YOU - LEARNING - 2
Explore 40 Videos
- HCF AND LCMBook:ARIHANT SSCChapter:HCF AND LCMExercise:Exercise Higher Skill Level Questions
Explore 18 Videos
Similar Questions
Knowledge Check
AD is angular bisector of AABC such that BD:DC = 2:3. If AB = 7cm, what is AC: BC?
A2:3B3:2C21:10DNone of theseIn ΔABC,AD is the inernal besector of ∠A. If BD = 5cm , BC=7.5 cm , then AB:AC=
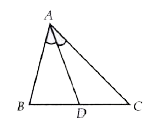 A2:1B1:2C4:5D3:5
A2:1B1:2C4:5D3:5In the given figure AC is bisector of ∠BAD, AB=3cm,AC=5cm, then AD= ______
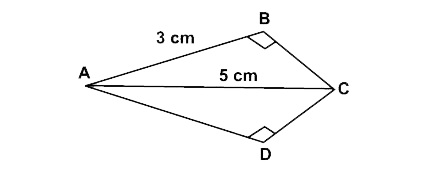 A2 cmB5 cmC3 cmD8 cm
A2 cmB5 cmC3 cmD8 cm
In the given figure , if AD is the bisector of ∠BAC . If AB=10 cm , AC = 14 cm and BC = 6 cm , then find BD and DC .

View SolutionIn △ABC, AD is the internal bisector of ∠S, meeting the side BC at D. If BD = 5cm, BC = 7.5 cm, then AB:AC is:
View SolutionIn figure AD is the bisector of ∠BAC. If BD=2cm,CD=3cmandAB=5cm. Find AC :
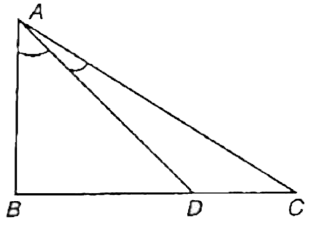
View SolutionAssertion (A) : AD is angle bisector of ∠A of the triangle ABC. If AB = 6 cm, BC = 7 cm, AC = 8 cm then BD = 3 cm and CD = 4 cm.
Reason (R) : The angle bisector AD of the triangle divides base BC in the ratio AB : AC.
View SolutionIf AD is the bisector of ∠BAC and AB = 10 cm, AC = 6 cm, BC = 12 cm, then find BD?
यदि AD, ∠BAC का समद्विभाजक है तथा AB = 10cm, AC = 6cm, BC = 12cm, तो BD ज्ञात करें।
View Solution

