Question

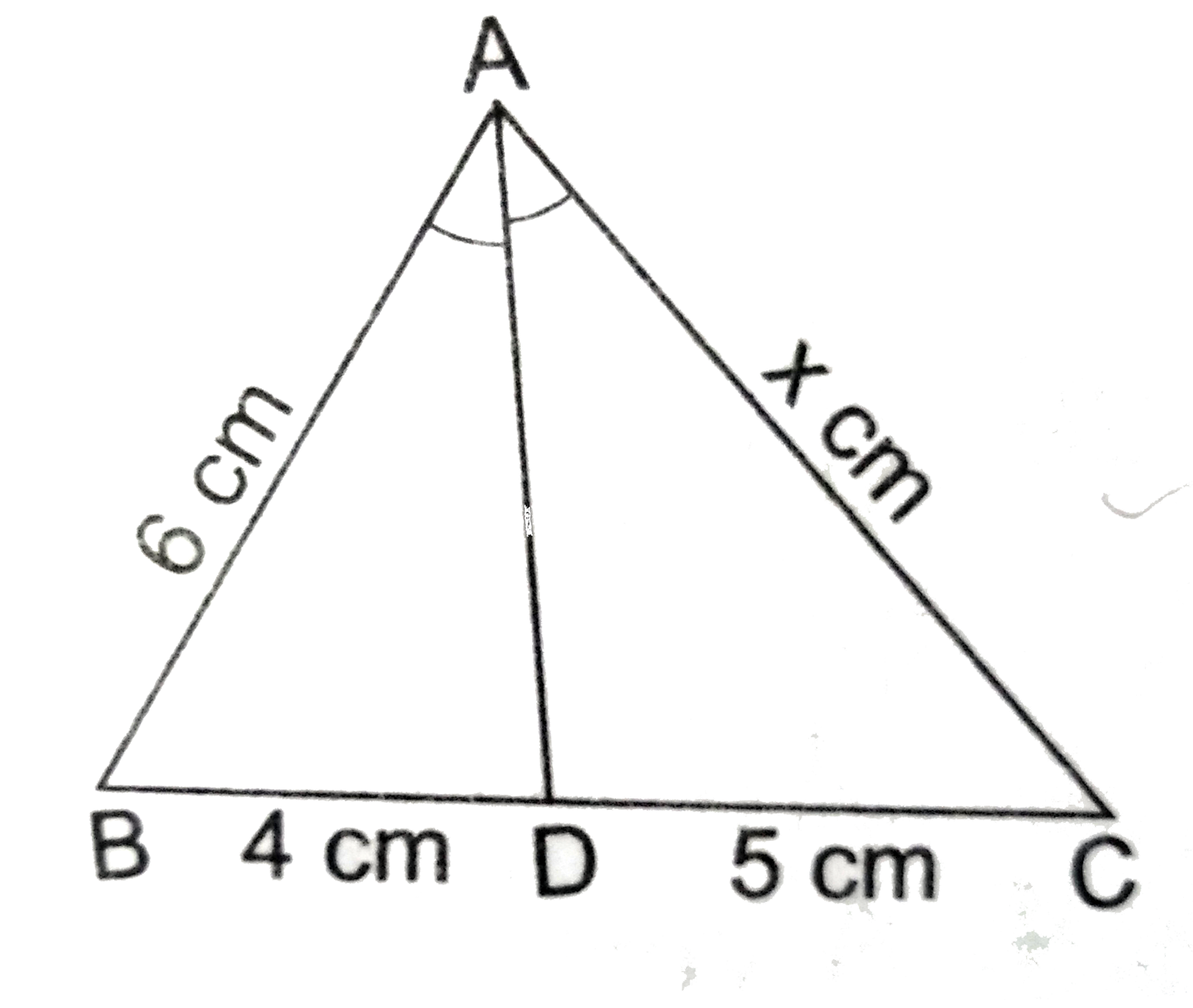
In $\Delta ABC$, AD is the internal bisector of $\angle A$, meeting the side BC at D. If $BD=5cm,BC=7.5cm$, then $AB:AC$is

Options

A. `2:1`
B. `1:2`
C. `4:5`
D. `3:5 `

Answer

A

Explanation

To solve the problem, we will use the Angle Bisector Theorem, which states that the ratio of the lengths of the two segments created by the angle bisector on the opposite side is equal to the ratio of the lengths of the other two sides of the triangle.

1. Identify the Given Information:
- In triangle ABC, AD is the internal bisector of angle A.
- BD = 5 cm
- BC = 7.5 cm

2. Determine the Length of DC:
- Since BC = BD + DC, we can find DC:
\( DC = BC - BD = 7.5 \, \text{cm} - 5 \, \text{cm} = 2.5 \, \text{cm} \)

3. Apply the Angle Bisector Theorem:
- According to the Angle Bisector Theorem:
\( \frac{AB}{AC} = \frac{BD}{DC} \)
- Substituting the known values:
\( \frac{AB}{AC} = \frac{5 \, \text{cm}}{2.5 \, \text{cm}} \)

4. Simplify the Ratio:
- Simplifying the fraction:
\( \frac{5}{2.5} = \frac{5 \div 2.5}{2.5 \div 2.5} = \frac{2}{1} \)

5. Conclusion:
- Therefore, the ratio \( AB : AC \) is \( 2 : 1 \).

Final Answer:
\( AB : AC = 2 : 1 \)