The equidistant point from the vertices of a triangle is called its :
Centroid
Incentre
Circumcentre
Orthocentre
The correct Answer is:C
To solve the question "The equidistant point from the vertices of a triangle is called its:", we can follow these steps:
1. Understanding the Triangle:
- Start by visualizing or drawing a triangle with vertices labeled as A, B, and C.
2. Identifying the Equidistant Point:
- We need to find a point that is equidistant from all three vertices (A, B, and C) of the triangle.
3. Defining the Point:
- Let’s denote the point that is equidistant from A, B, and C as point O. This means that the distance from O to A (OA), O to B (OB), and O to C (OC) are all equal.
4. Understanding the Circumcircle:
- If we draw a circle that passes through all three vertices A, B, and C, the center of this circle is the point O. This circle is known as the circumcircle of the triangle.
5. Naming the Point:
- The point O, which is equidistant from the vertices of the triangle, is called the Circumcenter of the triangle.
Final Answer:
The equidistant point from the vertices of a triangle is called its Circumcenter.
---
- Start by visualizing or drawing a triangle with vertices labeled as A, B, and C.
- We need to find a point that is equidistant from all three vertices (A, B, and C) of the triangle.
- Let’s denote the point that is equidistant from A, B, and C as point O. This means that the distance from O to A (OA), O to B (OB), and O to C (OC) are all equal.
- If we draw a circle that passes through all three vertices A, B, and C, the center of this circle is the point O. This circle is known as the circumcircle of the triangle.
- The point O, which is equidistant from the vertices of the triangle, is called the Circumcenter of the triangle.
The equidistant point from the vertices of a triangle is called its Circumcenter.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-IV)
Explore 35 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-V)
Explore 30 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-II)
Explore 25 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
Knowledge Check
The locus of a point which moves such that the sum of the squares of the distances from the three vertices of a triangle is constant, is a circle whose centre is at the:
AIncentre of the triangleBCentroid of the triangleCOrthocentre of the triangleDCircumcentre of the triangleThe coordinates of the point which is equidistant from "the three vertices of the △AOB is:
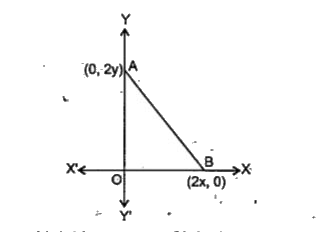 A(x,y)B(y,x)C(x2,y2)D(y2,x2)
A(x,y)B(y,x)C(x2,y2)D(y2,x2)A point P lying inside a triangle is equidistant from the vertices of the triangle. Then the triangle has P as its
ACentroidBIncentreCOrthocentreDCircumcentre
Prove that the locus of the point that moves such that the sum of the squares of its distances from the three vertices of a triangle is constant is a circle.
View SolutionProve that the locus of a point which moves such that the sum of the square of its distances from the vertices of a triangle is constant is a circle having centre at the centroid of the triangle.
View SolutionThe point of concurrence of the altitudes of a triangle is called
View SolutionThe coordinates of the point which is equidistant from the three vertices of the △AOB as shown in the figure is
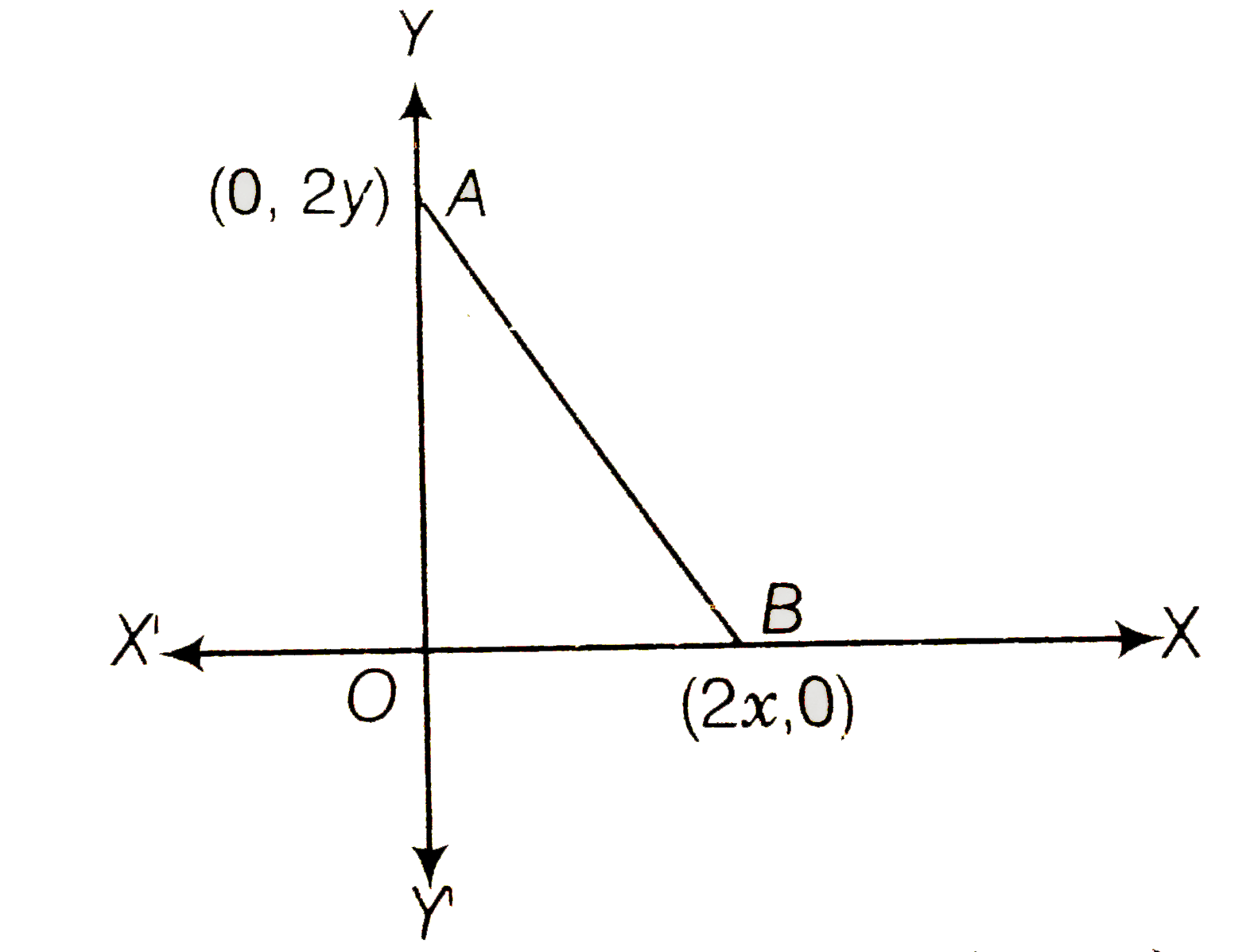
View SolutionThe locus of a point which moves such that the sum of the square of its distance from three vertices of a triangle is constant is a/an circle (b) straight line (c) ellipse (d) none of these
View Solution
