The measure of the angle between the internal and external bisectors of an angle is
60∘
70∘
80∘
90∘
The correct Answer is:D
To find the measure of the angle between the internal and external bisectors of an angle, we can follow these steps:
1. Understanding the Angle Bisectors:
- Let the angle be represented as ∠BOD where O is the vertex of the angle and B and D are points on the two rays forming the angle.
2. Define the Angle:
- Let ∠BOD=θ.
3. Internal Bisector:
- The internal bisector of the angle ∠BOD divides it into two equal parts. Therefore, the angle formed by the internal bisector and the rays is:
∠DOH=θ2
4. External Bisector:
- The external bisector of the angle ∠BOD is the line that divides the exterior angle ∠AOB (where A is a point on the extension of ray OB) into two equal parts. The angle ∠AOB is:
∠AOB=180∘−θ
- Thus, the angle formed by the external bisector and the rays is:
∠EOD=12(180∘−θ)=90∘−θ2
5. Finding the Angle Between Internal and External Bisectors:
- The angle between the internal bisector (line OH) and the external bisector (line OE) is given by:
∠EOH=∠EOD+∠DOH
- Substituting the values:
∠EOH=(90∘−θ2)+(θ2)
- Simplifying this gives:
∠EOH=90∘
6. Conclusion:
- Therefore, the measure of the angle between the internal and external bisectors of an angle is 90∘.
Final Answer:
The measure of the angle between the internal and external bisectors of an angle is 90∘.
---
- Let the angle be represented as ∠BOD where O is the vertex of the angle and B and D are points on the two rays forming the angle.
- Let ∠BOD=θ.
- The internal bisector of the angle ∠BOD divides it into two equal parts. Therefore, the angle formed by the internal bisector and the rays is:
∠DOH=θ2
- The external bisector of the angle ∠BOD is the line that divides the exterior angle ∠AOB (where A is a point on the extension of ray OB) into two equal parts. The angle ∠AOB is:
∠AOB=180∘−θ
- Thus, the angle formed by the external bisector and the rays is:
∠EOD=12(180∘−θ)=90∘−θ2
- The angle between the internal bisector (line OH) and the external bisector (line OE) is given by:
∠EOH=∠EOD+∠DOH
- Substituting the values:
∠EOH=(90∘−θ2)+(θ2)
- Simplifying this gives:
∠EOH=90∘
- Therefore, the measure of the angle between the internal and external bisectors of an angle is 90∘.
The measure of the angle between the internal and external bisectors of an angle is 90∘.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-IV)
Explore 35 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-V)
Explore 30 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-II)
Explore 25 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
Knowledge Check
If one of the angles of a triangle is 62, then the angle between the exterior bisectors of the other two angles is
A31∘B59∘C121∘D118∘If one of the angles of a triangles is 120∘ , then the angle between the interior bisectors of the other two angles is
A90∘B30∘C150∘D60∘In the given figure, if AB is the diameter of the circle and PM the internal bisector of ∠APB, then the measure of angle ABM is
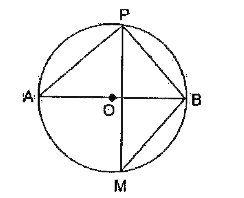 A15∘B30∘C45∘D60∘
A15∘B30∘C45∘D60∘
If h,m1,n1andl2,m2,n2areD.C.s of the two lines inclined to each other at an angle θ, then the D.C.'s of the internal and external bisectors of the angle between these lines are-
View SolutionShow that, in a parallelogram ABCD, the internal and external bisectors of ∠Aand∠B from a rectangle.
View SolutionThe sides of a triangle ABC are 6, 7, 8, the smallest angle being C then
The length of internal bisector of angle C is …
View SolutionBisector of angle between the pair of lines
View SolutionThe vertices of a triangle are A(1,1,2),B(4,3,1) and C(2,3,5) Vectors representing the internal & external bisectors of the angle A are:
View Solution
