Question

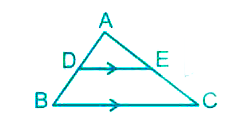
In $\Delta ABC$ DE||BC, where DE intersects AB and AC at the points D and E, respectively. If AD = 6 cm, DB = 12X- 6cm, AE= 2x cm and CE = 16 - 2x cm, then the value of X is

Options

A. 6 cm
B. 4 cm
C. 2 cm
D. 8 cm

Answer

C

Explanation

To solve the problem, we will use the properties of similar triangles and the concept of proportionality. Given that DE is parallel to BC, we can set up a proportion based on the segments created by the intersection of DE with AB and AC.

1. Identify the segments:
- We have AD = 6 cm
- DB = 12x - 6 cm
- AE = 2x cm
- CE = 16 - 2x cm

2. Write the expressions for AB and AC:
- The length of AB can be expressed as:
\( AB = AD + DB = 6 + (12x - 6) = 12x \)
- The length of AC can be expressed as:
\( AC = AE + CE = 2x + (16 - 2x) = 16 \)

3. Set up the proportion:
Since DE is parallel to BC, we can use the property of similar triangles:
\( \frac{AD}{DB} = \frac{AE}{CE} \)
Substituting the values we have:
\( \frac{6}{12x - 6} = \frac{2x}{16 - 2x} \)

4. Cross-multiply to eliminate the fractions:
\( 6(16 - 2x) = 2x(12x - 6) \)
Expanding both sides:
\( 96 - 12x = 24x^2 - 12x \)

5. Rearranging the equation:
Move all terms to one side:
\( 24x^2 - 12x - 96 + 12x = 0 \)
Simplifying gives:
\( 24x^2 - 96 = 0 \)

6. Factor out the common term:
\( 24(x^2 - 4) = 0 \)
This simplifies to:
\( x^2 - 4 = 0 \)

7. Solve for x:
\( x^2 = 4 \)
Taking the square root of both sides gives:
\( x = 2 \quad \text{or} \quad x = -2 \)
Since x represents a length, we only consider the positive value:
\( x = 2 \)

Final Answer:
The value of \( x \) is \( 2 \) cm.

---