Assertion (A) : AD is angle bisector of ∠A of the triangle ABC. If AB = 6 cm, BC = 7 cm, AC = 8 cm then BD = 3 cm and CD = 4 cm.
Reason (R) : The angle bisector AD of the triangle divides base BC in the ratio AB : AC.
Both Assertion A and Reason R are correct and Reason R is a correct explanation of Assertion A.
Both Assertion A and Reason R are correct but Reason R is not the correct explanation of Assertion A.
Assertion A is correct, Reason R is wrong.
Assertion A is wrong, Reason R is correct.
The correct Answer is:A
To solve the problem, we will analyze the assertion and reason provided in the question step by step.
Step 1: Understand the Assertion
The assertion states that AD is the angle bisector of angle A in triangle ABC, with the following dimensions:
- AB = 6 cm
- AC = 8 cm
- BC = 7 cm
- BD = 3 cm
- CD = 4 cm
Step 2: Verify the Angle Bisector Theorem
According to the Angle Bisector Theorem, the angle bisector of an angle in a triangle divides the opposite side into segments that are proportional to the other two sides. This means:
ABAC=BDDC
Step 3: Calculate the Ratios
Now, we will calculate the ratios using the given lengths:
- AB=6 cm
- AC=8 cm
- BD=3 cm
- DC=4 cm
Calculating the left side of the equation:
ABAC=68=34
Now, calculating the right side of the equation:
BDDC=34
Step 4: Compare the Ratios
Since both ratios are equal:
ABAC=BDDC⟹34=34
This confirms that the assertion is correct.
Step 5: Analyze the Reason
The reason states that the angle bisector AD divides the base BC in the ratio of AB to AC. Since we have already established that the angle bisector divides the opposite side in the ratio of the adjacent sides, the reason correctly explains the assertion.
Conclusion
Both the assertion and the reason are true, and the reason is indeed the correct explanation for the assertion.
Final Answer
- Assertion (A): True
- Reason (R): True
- Explanation: The angle bisector divides the opposite side in the ratio of the adjacent sides.
---
The assertion states that AD is the angle bisector of angle A in triangle ABC, with the following dimensions:
- AB = 6 cm
- AC = 8 cm
- BC = 7 cm
- BD = 3 cm
- CD = 4 cm
According to the Angle Bisector Theorem, the angle bisector of an angle in a triangle divides the opposite side into segments that are proportional to the other two sides. This means:
Now, we will calculate the ratios using the given lengths:
- AB=6 cm
- AC=8 cm
- BD=3 cm
- DC=4 cm
Since both ratios are equal:
The reason states that the angle bisector AD divides the base BC in the ratio of AB to AC. Since we have already established that the angle bisector divides the opposite side in the ratio of the adjacent sides, the reason correctly explains the assertion.
Both the assertion and the reason are true, and the reason is indeed the correct explanation for the assertion.
- Assertion (A): True
- Reason (R): True
- Explanation: The angle bisector divides the opposite side in the ratio of the adjacent sides.
Topper's Solved these Questions
- CENTRE OF TRIANGLEBOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B
8 Videos
- CENTRE OF TRIANGLEBOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B
8 Videos
- ALGEBRAIC IDENTITIES BOOK - LUCENT PUBLICATIONCHAPTER - ALGEBRAIC IDENTITIES EXERCISE - Exercise - 1B
28 Videos
- CIRCLE AND ITS TANGENT LINESBOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B
27 Videos
Similar Questions
Knowledge Check
In △ABC,AB=6cm,AC=8cm,andBC=9cm. The length of median AD is :
A√3172cmB√1192cmC√1152cmD√3132cmIn figure AD is the bisector of ∠BAC. If BD=2cm,CD=3cmandAB=5cm. Find AC :
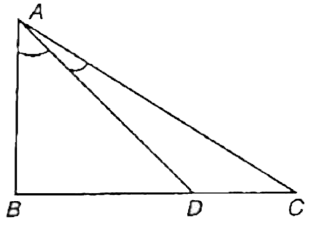 A6 cmB7.5 cmC10 cmD15 cm
A6 cmB7.5 cmC10 cmD15 cmAD is angular bisector of AABC such that BD:DC = 2:3. If AB = 7cm, what is AC: BC?
A2:3B3:2C21:10DNone of these
If in △ABC, AD is the bisector of ∠AandD lies on BC. If AB = 6.4 cm, AC = 8 cm, BD = 5.6 cm, find DC.
View SolutionProve xa>yb if x>y and b<0 .
View SolutionCan we construct a triangle ABC in which AB=3 cm, BC=4 cm and AC=8 cm ?
View SolutionIn △ABC, AD is the internal bisector of ∠S, meeting the side BC at D. If BD = 5cm, BC = 7.5 cm, then AB:AC is:
View SolutionIn ΔABC, AD is the internal bisector of ∠A, meeting the side BC at D. If BD=5cm,BC=7.5cm, then AB:ACis
View Solution
