In the given figure (not to scale), PQ is a tangent segment , drawn to the circle with centre O at P and QR =RO. iF PQ=3√3cm, and ORQ is a line segment, then find the radius of the circle.
(a) √3cm
(b) 3cm
(c) 2√3cm
(d) 2cm

Let radius of the circle be x.
∴OR=RQ=x(givenOR=RQ)
Join OP
∴¯¯¯¯¯¯OP⊥¯¯¯¯¯¯PQ
OP2+PQ2=OQ2
⇒x2+(3√3)2=(2x)2
⇒3x2=27⇒x2=9⇒x=±3
But x is positive.
∴x=3cm.

Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Test Yours concepts very shory answer type questions
29 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Short answer type questions
13 Videos
- BANKING BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - BANKING EXERCISE - LEVEL 3
10 Videos
- LIMITSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIMITSEXERCISE - LEVEL-3
15 Videos
Similar Questions
Knowledge Check
In the adjoining figure, the length of BC is
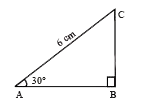
(a)2√3 cm
(b)3√3 cm
(c)4√3 cm
(d)3 cmA2√3 cmB3√3 cmC4√3 cmD3 cmIn the figure given, the radius of circle is (PS=12 cm, PQ=8 cm)
 A8 cmB5 cmC4 cmD10 cm
A8 cmB5 cmC4 cmD10 cmIn the given figure, PQ is the tangent of the circle. Line segment PR intersects the circle at N and R. PQ=15cm,PR=25cm, find PN:
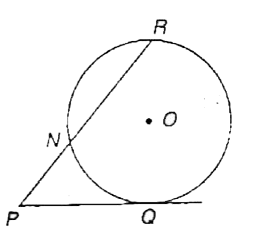 A15 cmB10 cmC9 cmD6 cm
A15 cmB10 cmC9 cmD6 cm
In the figure, segment QR is a tangent to the circle with centre P.PR = 12 cm and PQ = 6 cm. Find the area of shaded region. (√3=1.73,π=3.14)
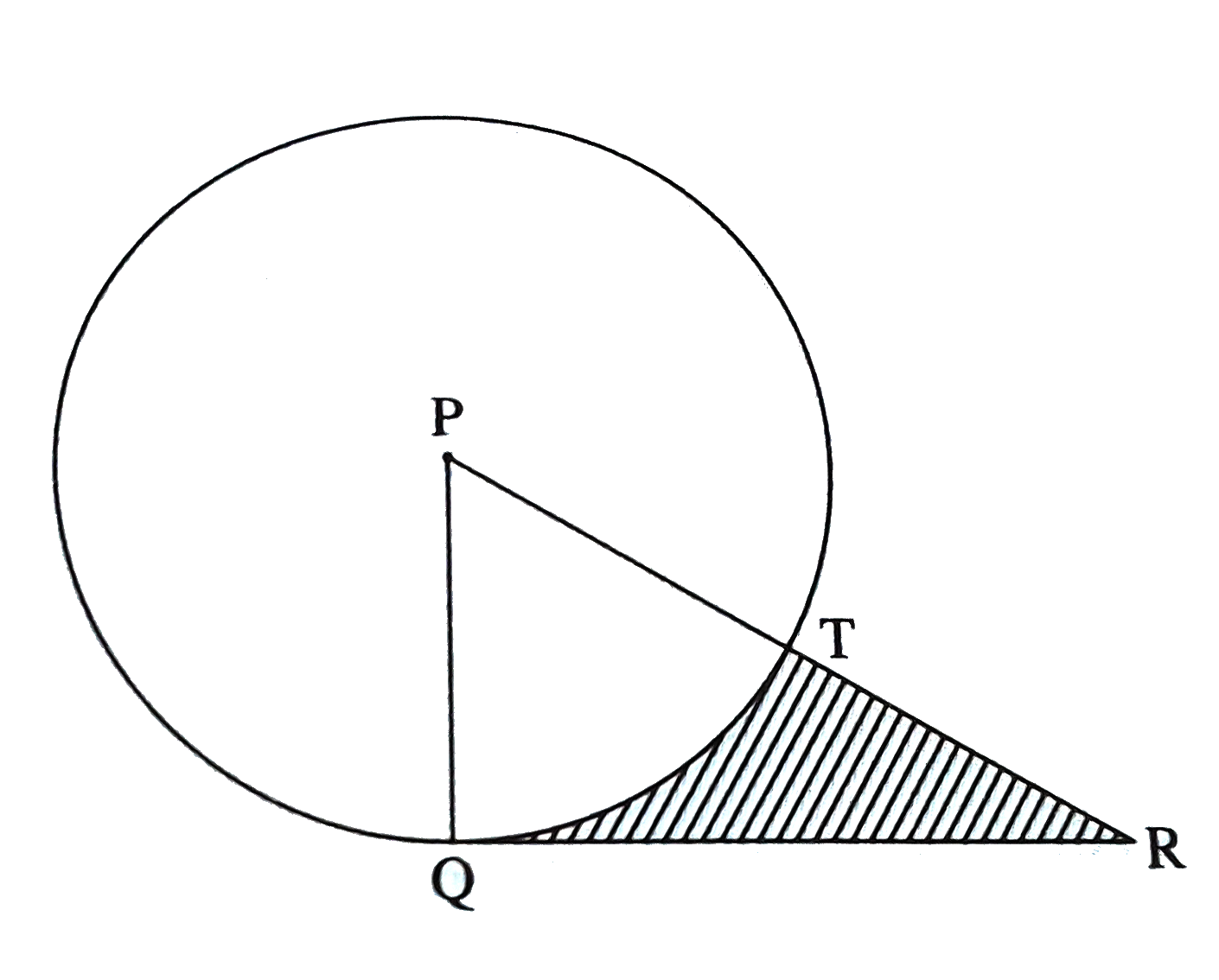
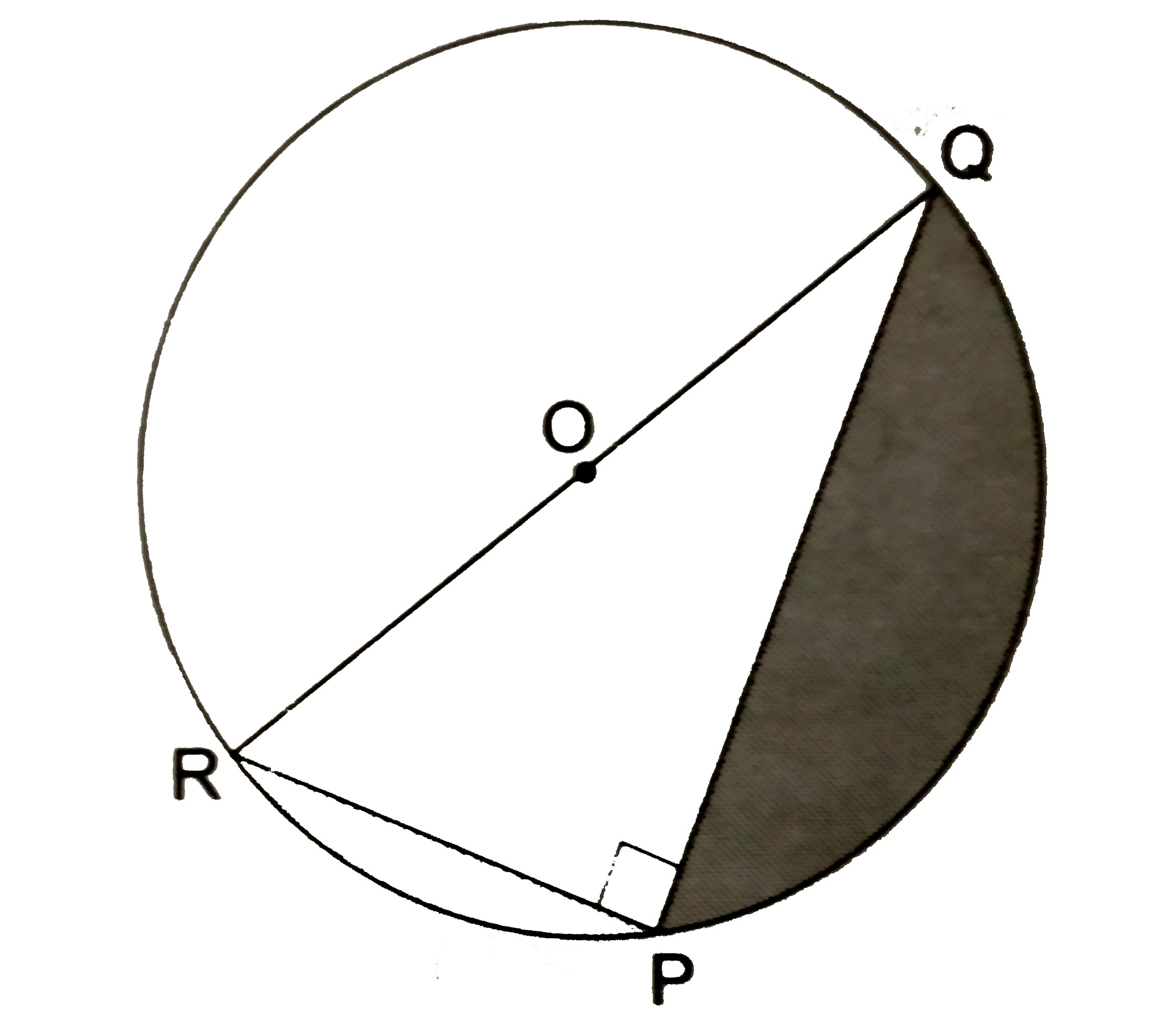
View SolutionIn the given figure, PQ = 24 cm PR = 7 cm and O is the centre of the circle. Find the area of the shaded region. (Use π=3.14)

View SolutionIn the given figure PQ=24cm,PR=78cm and O is the centre of the circle. Find the area of the shaded region. [Take π=3.14]
View SolutionPQR is a right angled triangle at Q with QR =12 a=cm and PQ=5cm. A circle with centre O is inscribed in △PQR. Find the radius of the circle.
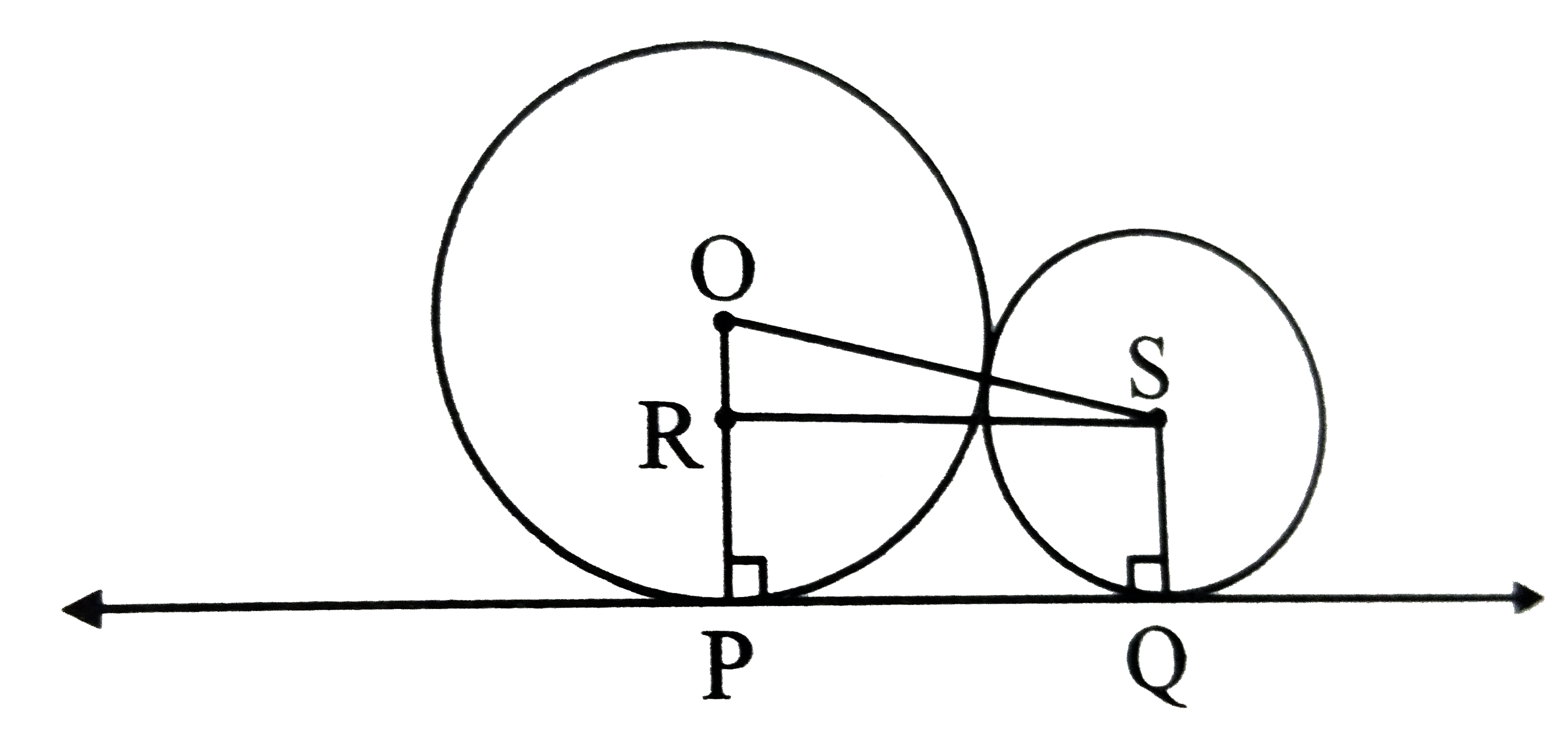
View SolutionIn the adjoining figure , line PQ is a common tangent to the externally touching circles and the radii of two circles are 25cm and 9cm. Find the length of the common tangent segment of these circles.
View Solution