In the given figure ¯¯¯¯¯¯DE∣∣¯¯¯¯¯¯AC. Find the value of x.
(a)1(b)2(c)3(d)4
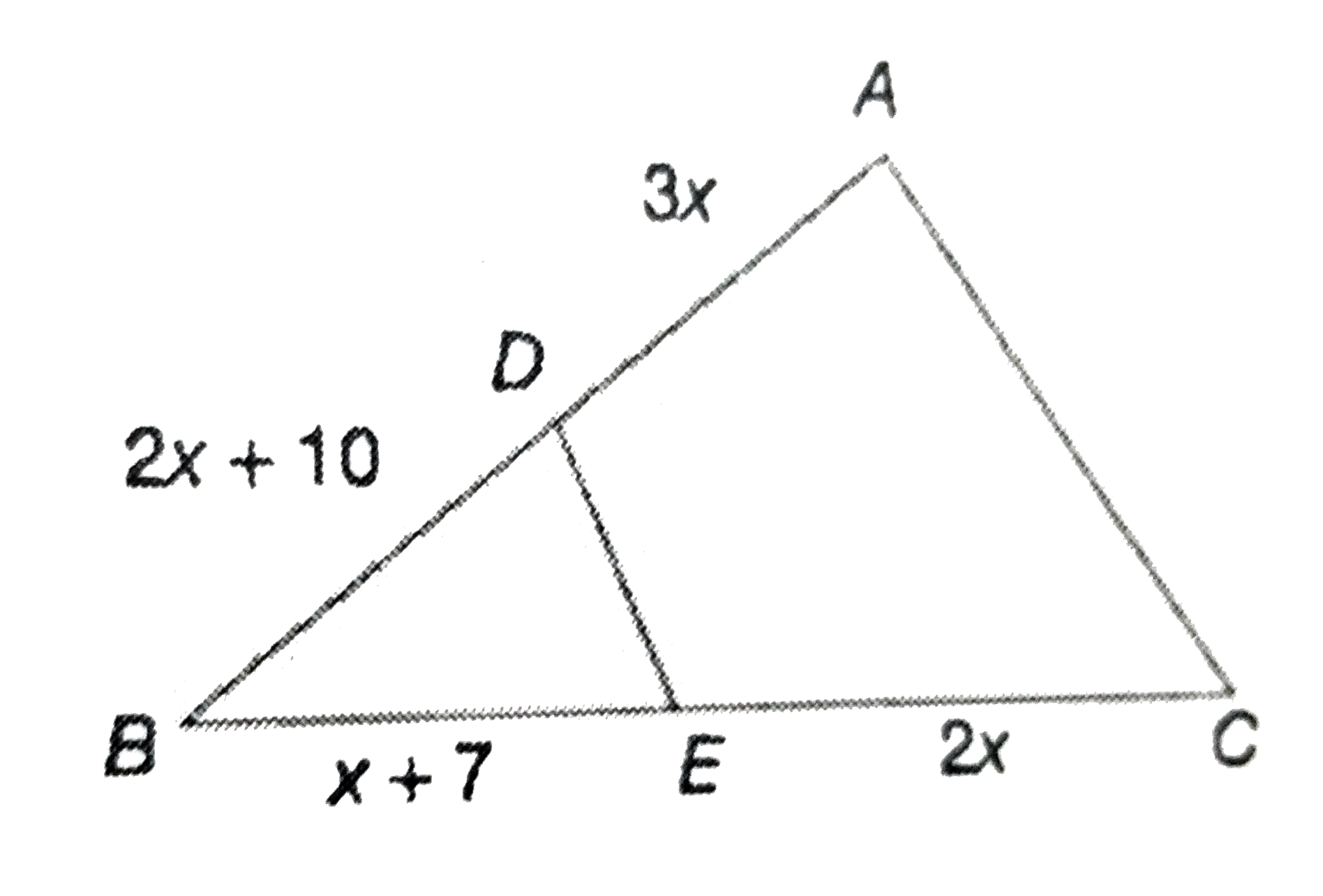
In ∠ABC,
DE∣∣AC
∴BDDA=BEEC (Basic proportionality theorem)
⇒2x+103x=x+72x
⇒2x(2x+10)=3x(x+7)
⇒4x2+20x=3x2+21x
⇒x2−x=0
⇒x(x−1)=0
⇒x−1=0
⇒x=1
∴ Hence, option (a) is the correct answer.
Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Test Yours concepts very shory answer type questions
29 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Short answer type questions
13 Videos
- BANKING BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - BANKING EXERCISE - LEVEL 3
10 Videos
- LIMITSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIMITSEXERCISE - LEVEL-3
15 Videos
Similar Questions
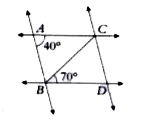
In the above figure (not to scale) , ¯¯¯¯¯¯AB∣∣∣∣¯¯¯¯¯¯CDand¯¯¯¯¯¯AC∣∣∣∣¯¯¯¯¯¯BD. If ∠BAC=40∘and∠CBD=70∘, then ∠BCD=_______.
View SolutionLet ¯a be vectors parallel to line of intersection of planes p1andp2 through origin. If p1 is parallel to the vectors 2¯j+3¯kand4¯j−3¯kandp2 is parallel to ¯j−¯kand3¯i−3¯j, then the angle between ¯aand2¯i+¯j−2¯k is (A) π2 (B) π4 (C) π3 (D) π6
View Solution
Knowledge Check
In the above figure, ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯DE and ACE is a straight line . I f ∠ABC=30∘ and ∠CDE=20∘, then find ∠BCD.A40∘B50∘C60∘D70∘Find the sum of 3.¯2 and 5.¯4.
A783B583C589D789
In the above figure , ¯¯¯¯¯¯ABand¯¯¯¯¯¯AC are equal chords and ¯¯¯¯¯¯OD is perpendicular to ¯¯¯¯¯¯AC . If ∠COD=60∘, then the angle between the chords is ______ .A30∘B60∘C90∘D45∘
If ¯c=2¯a+5¯b,|¯a|=a,∣∣¯b∣∣=b and the angle between ¯aand¯b is π3, then c2=
View SolutionIn triangle ABC, if 2¯¯¯¯¯¯AC=3¯¯¯¯¯¯CB, then 2¯¯¯¯¯¯OA+3¯¯¯¯¯¯OB=
View SolutionIf ¯c=3¯a−2¯b, then [¯a¯b¯c]=
View Solution[¯a¯b¯c] is the scalar triple product of three vectors ¯a,¯b,¯c then [¯a¯b¯c]=
View SolutionThe volume of the paralleloP1ped whose co-terminous edges are ¯a,¯b,¯c, where ¯a,¯b,¯c are non-coplanar units vectors each inclined with other at an angle of 60∘ is
View Solution
