Question

Discuss the number of roots of the equation ${\displaystyle e(k-x\log x)=1}$
for different value of ${\displaystyle k\stackrel{.}{}}$

Explanation

`e(k-xlogx)=1`
`rArr k-1/e=xlogx`
Then Eq. (i) has solution where the graphs of `y=x logx `and `y=k-1/e` intersects. Now, consider the function `f(x) = xlog_(e)x`
`f(x)=0 therefore x=1`
`f(x) gt 0` for `x gt 1`
`f(x) lt 0` for `0 lt x lt 1`
`underset(x to 0+)"lim"(x.log_(e)x) (0 xx infty"form")`
`=underset(xto 0+)"lim"(1/x)/(-1/x^(2)) = underset(xto 0+)"lim"(-x)=0`
Now `f^(')(x)=x.1/x + log_(e)x=1+log_(e)x`
`f^(')(x)=0 therefore f^('')(1//e) =e gt0`, so `x=1//e` is the point of minima.
`f(x)` decreases in `(0,1/e)` from 0 to `-1/e` and increases in `(1/e, infty)` from `-1/e` to `infty`, intersecting the x-axis at (1,0)
Hence the graph of `f(x)=xlog_(e)x` is as shown in the following figure.

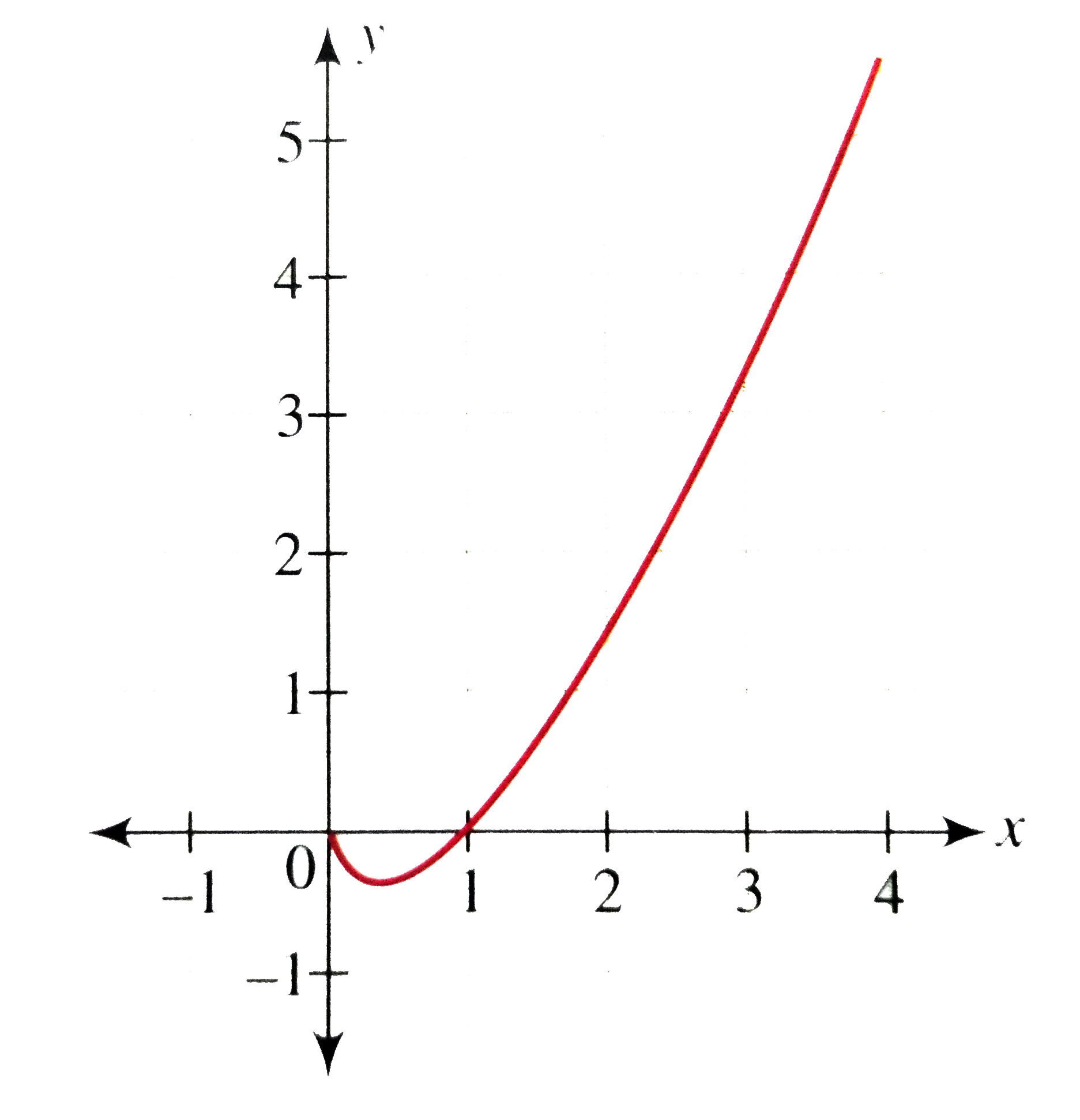
Hence, the graph of `f(x) = xlog_(e)x` is as shown in the following figure.
Hence the equation `k-1/e=xlog_(e)x` has two distinct roots.
if `-1/e lt k - 1/e lt 0 rArr 0 lt k lt 1/e`
The equation has no roots if `k-1/e lt -1/e rArr k lt 0`
The equation has one root if `k-1/e=1/e` or `k-1/e ge0 rArr =0` or `k ge1/e`