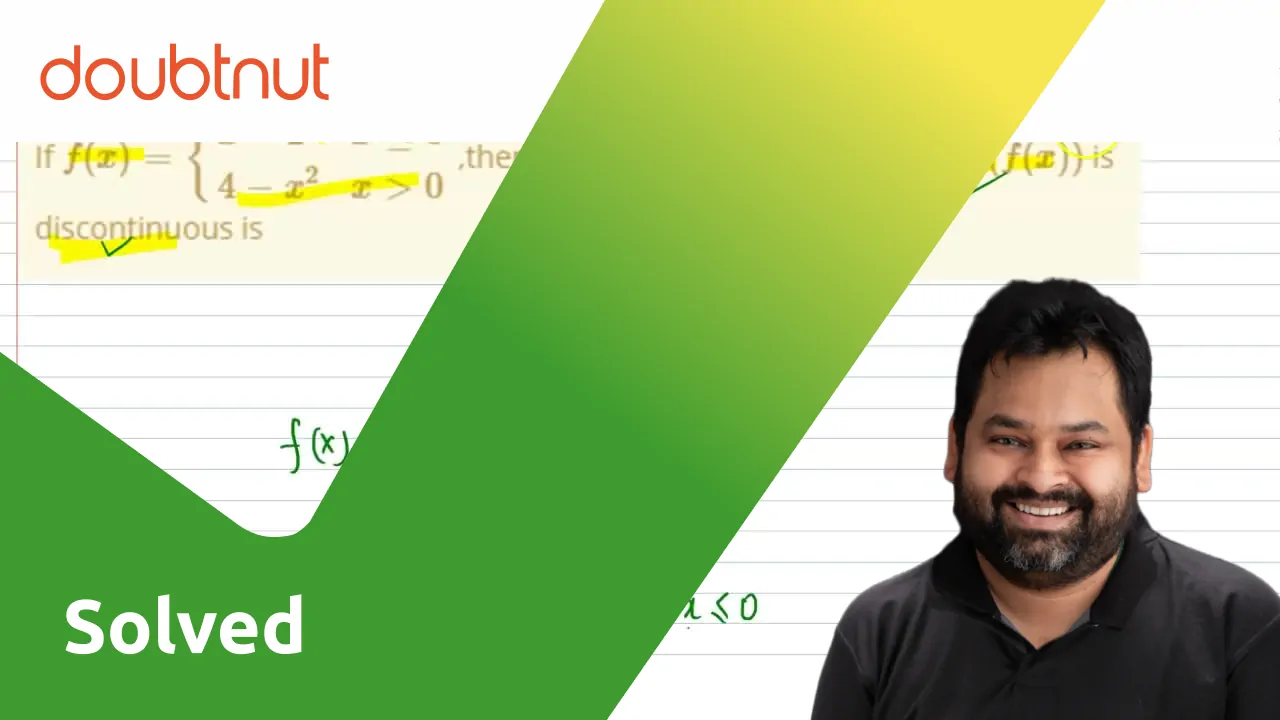
If f(x)={x−2x≤04−x2x>0 ,then number of points, where y=f(f(x)) is discontinuous is
Step by step video & image solution for If f(x)={:{ (x-2 ,x <= 0), (4-x^(2),x>0) :} ,then number of points, where y=f(f(x)) is discontinuous is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
Find all points of discontinuity of f, where f is defined by f(x) = {{:((|x|)/(x)," if "x ne0),(0," if "x= 0):}
05:23View SolutionFind all points of discontinuity of f, where f is defined byf(x)={x|x|ifx<01ifx≥0
04:13View SolutionLet g(x)=f(f(x)) where f(x)={1+x;0≤x≤2}andf(x)={3−x;2<x≤3} then the number of points of discontinuity of g(x) in [0,3] is :
04:49View SolutionFind all points of discontinuity of f, where f is defined by : f(x)={|x|xifx≠00ifx=0
06:55View SolutionFind all points of discontinuity of f, where f is defined by: f(x)={x|x|ifx<0−1ifx≥0
05:01View SolutionFind all points of discontinuity of f, where: f(x)={sinxxifx<0x+1ifx≥0
08:03View Solutionfind the points of discontinuity of the function f defined by f(x) = {(|x|/x, x ne 0),(0,x=0):}
03:34View SolutionFind all points of discontinuity of f, where f is defined by f(x) = {{:((|x|)/(x), "if" x != 0),(0,"if" x = 0):}
06:55View Solution