In a △ABC the angles at B and C are acute. If BE and CF be drawn perpendiculars on AC and AB respectivel, prove that
BC2=Ab×BF+AC×EC
To prove that in triangle ABC, where BE and CF are perpendiculars from points B and C to sides AC and AB respectively, the equation BC2=AB⋅BF+AC⋅EC holds, we can follow these steps:
1. Identify the Right Triangles:
- We have two right triangles: △BFC and △BEC.
- In △BFC, BF is perpendicular to AC.
- In △BEC, BE is perpendicular to AB.
2. Apply the Pythagorean Theorem:
- For triangle BFC:
BC2=BF2+FC2(1)
- For triangle BEC:
BC2=BE2+EC2(2)
3. Add the Two Equations:
- Adding equations (1) and (2):
2BC2=BF2+FC2+BE2+EC2(3)
4. Express BF and FC:
- From triangle ABF:
BF=AB−AF(4)
- From triangle AEC:
EC=AC−AE(5)
5. Substitute BF and EC into the Equations:
- Substitute (4) and (5) into equation (3):
2BC2=(AB−AF)2+(AC−AE)2+BE2+EC2
6. Expand the Squares:
- Expanding the squares:
(AB−AF)2=AB2−2AB⋅AF+AF2
(AC−AE)2=AC2−2AC⋅AE+AE2
7. Combine and Simplify:
- Combine all the terms:
2BC2=AB2+AC2−2AB⋅AF−2AC⋅AE+AF2+BE2+AE2
8. Cancel Out Terms:
- Notice that some terms will cancel out, leading to:
BC2=AB⋅BF+AC⋅EC
9. Conclusion:
- Therefore, we have shown that:
BC2=AB⋅BF+AC⋅EC
- We have two right triangles: △BFC and △BEC.
- In △BFC, BF is perpendicular to AC.
- In △BEC, BE is perpendicular to AB.
- For triangle BFC:
BC2=BF2+FC2(1)
- For triangle BEC:
BC2=BE2+EC2(2)
- Adding equations (1) and (2):
2BC2=BF2+FC2+BE2+EC2(3)
- From triangle ABF:
BF=AB−AF(4)
- From triangle AEC:
EC=AC−AE(5)
- Substitute (4) and (5) into equation (3):
2BC2=(AB−AF)2+(AC−AE)2+BE2+EC2
- Expanding the squares:
(AB−AF)2=AB2−2AB⋅AF+AF2
(AC−AE)2=AC2−2AC⋅AE+AE2
- Combine all the terms:
2BC2=AB2+AC2−2AB⋅AF−2AC⋅AE+AF2+BE2+AE2
- Notice that some terms will cancel out, leading to:
BC2=AB⋅BF+AC⋅EC
- Therefore, we have shown that:
BC2=AB⋅BF+AC⋅EC
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a
23 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
In ΔABC,∠Band∠C are acute angles. BE and CF are perpendicular from vertices B and C on sides AC and AB respectively. Then BC2 is equal to-
View SolutionAD is a median of △ABC. The bisectors of ∠ADBand∠ADC meets AB and AC in E and F respectively prove that EF||BC.
View SolutionABC is a triangle in which altitude BE and CF drawn on AC and AB respectively are equal. Prove that ΔBEC≅ΔCFB
View SolutionIf in a triangle ABC, BE and CF are two medians perpendicular to each other and if AB=19 cm and AC=22cm then the length of BC is
View SolutionIn figure, DE||ABandBD||BEF. Prove that DC2=CF×AC
View SolutionIn ABC, D and E are points on sides AB and AC respectively such that AD×EC=AE×DB . Prove that DEBC .
View SolutionIn the given, if AB = AC. prove the BE = EC.
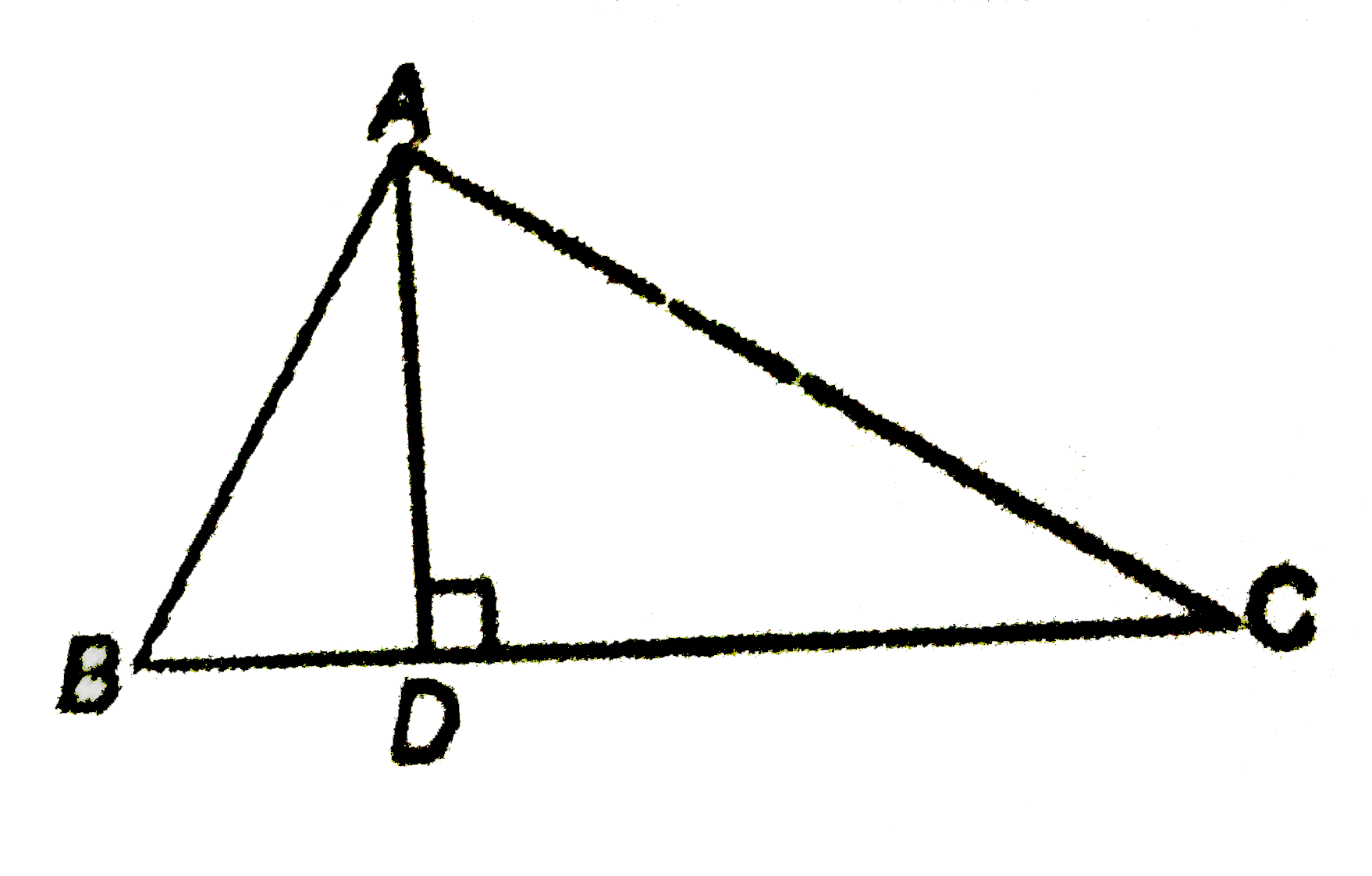
View SolutionIn the figure, AD is perpendicular to BC, prove that AB+AC>2AD.
View SolutionIf A. B and C are three points on a line, and B lies between A and C then prove that AB−BC=AC.
View SolutionIn a △ABC P and Q are points on AB and AC respectively and PQ||BC. Prove that the median AD bisects PQ.
View Solution
