are two triangles on the same base BC. A and D lies on opposite sides of BC. Prove that
Step by step video, text & image solution for triangleABC and triangleDBC are two triangles on the same base BC. A and D lies on opposite sides of BC. Prove that (ar(triangleABC))/(ar(triangleDBC))= (AO)/(DO) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Revision Exercise Short Questions
10 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
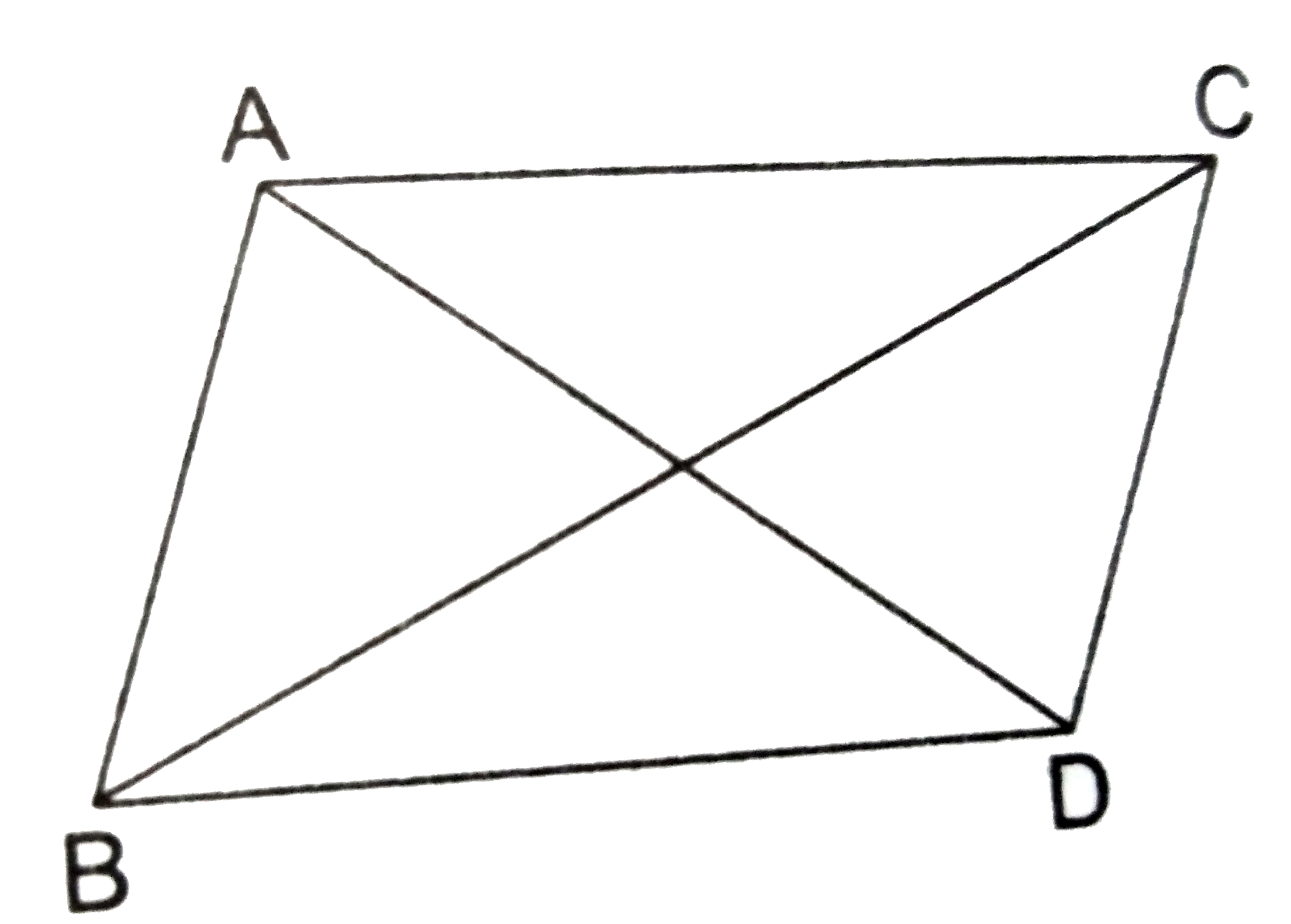
In the adjoining figure, △ABCand△DBC are on the same base BC with A and D on opposite sides of BC such that ar(△ABC)=ar(△DBC). Show that BC bisect AD.
View Solution△ ABC and △ DBC are isosceles triangles on the same base BC. Prove that line AD bisects BC at right angles
View SolutionIn figure, ABC and ABD are two triangles on the same base AB. If line segment CD is bisected by AB at O , show that ar(△ABC)=ar(△ABD).
View SolutionABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).

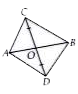
View SolutionIn Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)= AODO
View SolutionIn the same figure, ΔABCandΔDBC are on the same base BC . If AD is intersects BC at O, prove that
ar(ΔABC)ar(ΔDBC)=AODO
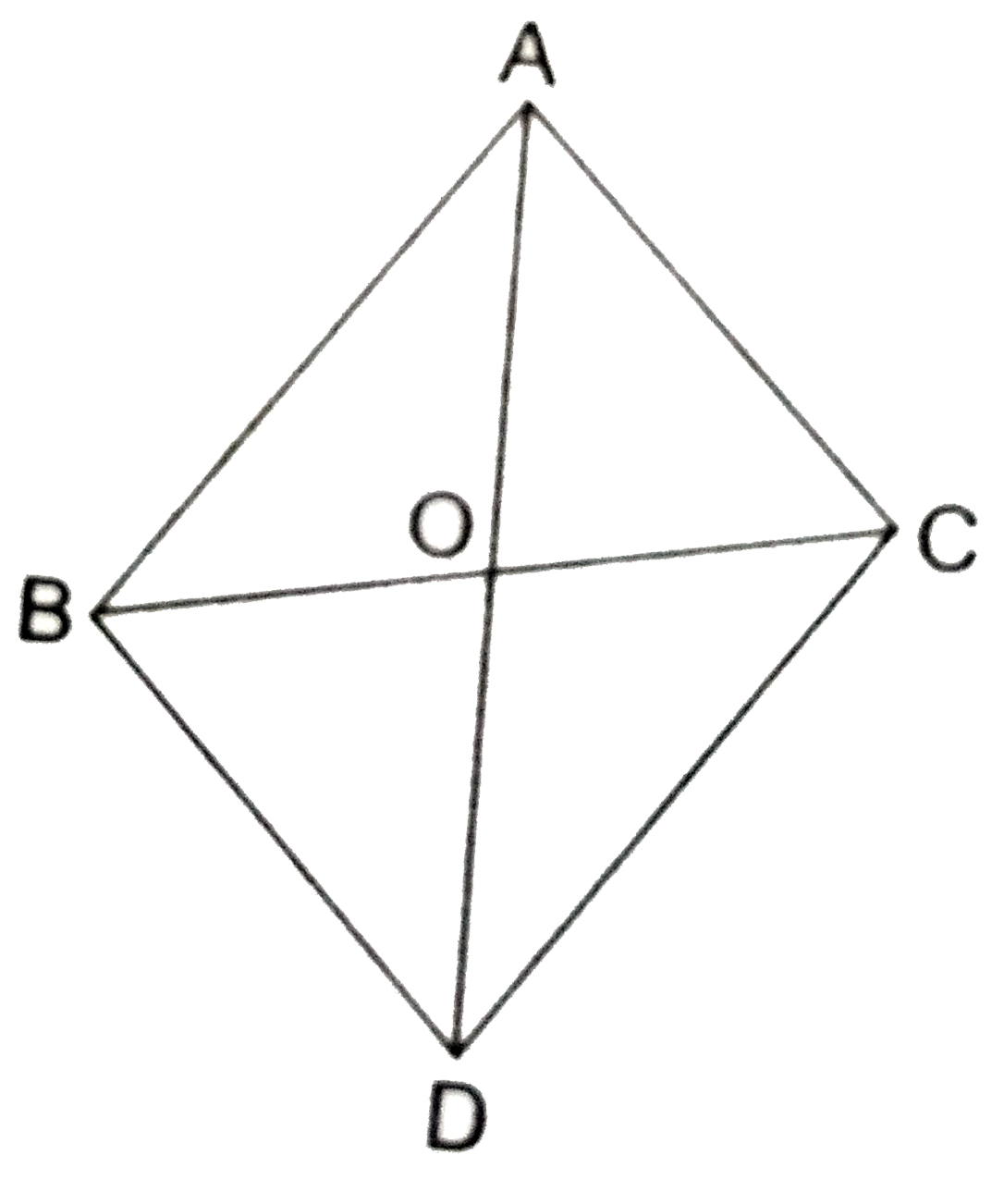
View SolutionIn the given figure, ΔABCandΔDBC are on the same base BC. If AD intersects BC at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
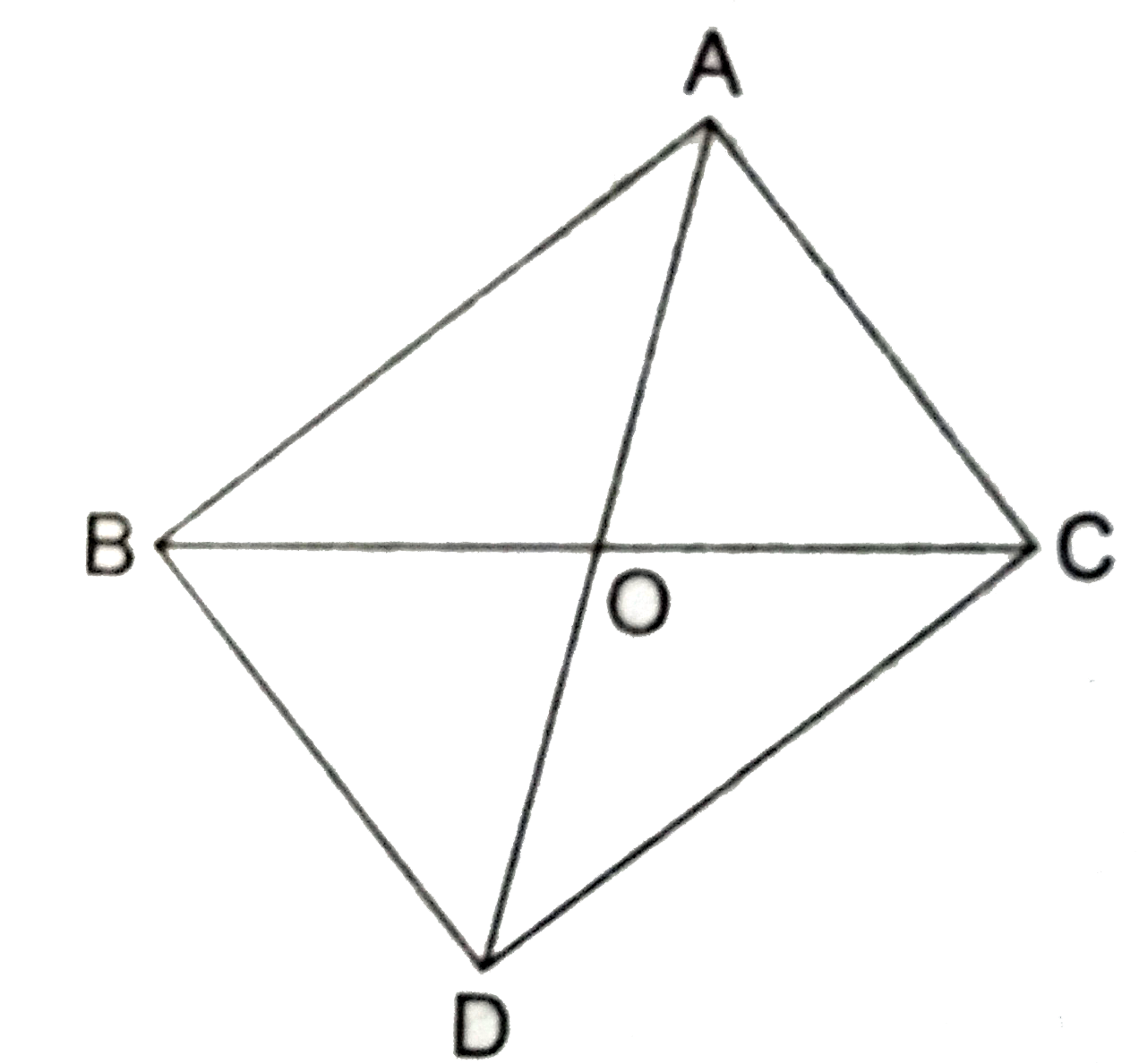
View SolutionIn the given figure, ΔABCandΔDBC have the same base BC. If AD and BC intersect at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
View SolutionABC and DBC are two triangle on the same base BC such that A and D lie on the opposite sides of BC,AB=AC and DB =DC ,Show that AD is the perpedicular bisector of BC.
View SolutionThe vertex A of △ABC is joined to a point D on the side BC. The midpoint of AD is E.
Prove that ar(△BEC)=12ar(△ABC).
View Solution
