ABC is a triangle in which altitude BE and CF drawn on AC and AB respectively are equal. Prove that ΔBEC≅ΔCFB
The correct Answer is:5.5 cm
To prove that triangles △BEC and △CFB are congruent, we will use the criteria for congruence of triangles, specifically the RHS (Right angle-Hypotenuse-Side) criterion.
1. Identify the Given Information:
- We have triangle ABC.
- Altitudes BE and CF are drawn from points B and C to sides AC and AB respectively.
- It is given that BE=CF.
Hint: Write down all the given information clearly to visualize the problem.
2. Draw the Triangle:
- Sketch triangle ABC with points B and C at the vertices, and draw the altitudes BE and CF to sides AC and AB.
Hint: Visualizing the triangle helps in understanding the relationships between the segments.
3. Identify Right Angles:
- Since BE and CF are altitudes, we know that:
∠BEC=90∘and∠CFB=90∘
Hint: Remember that altitudes create right angles with the base.
4. State the Equal Lengths:
- From the problem statement, we know:
BE=CF
Hint: Identify and write down all equal lengths as they will be crucial for proving congruence.
5. Identify the Common Side:
- The side BC is common to both triangles △BEC and △CFB:
BC=BC(common side)
Hint: Look for sides that are shared between the two triangles.
6. Apply the RHS Congruence Criterion:
- We have established:
- ∠BEC=90∘
- ∠CFB=90∘
- BE=CF
- BC=BC (common side)
- Therefore, by the RHS criterion (Right angle, Hypotenuse, Side), we can conclude:
△BEC≅△CFB
Hint: Recall the RHS criterion: if two triangles have one right angle, the hypotenuse is equal, and one side is equal, they are congruent.
7. Conclusion:
- Hence, we have proved that △BEC is congruent to △CFB.
Hint: Always summarize your findings to reinforce the conclusion.
- We have triangle ABC.
- Altitudes BE and CF are drawn from points B and C to sides AC and AB respectively.
- It is given that BE=CF.
- Sketch triangle ABC with points B and C at the vertices, and draw the altitudes BE and CF to sides AC and AB.
- Since BE and CF are altitudes, we know that:
∠BEC=90∘and∠CFB=90∘
- From the problem statement, we know:
BE=CF
- The side BC is common to both triangles △BEC and △CFB:
BC=BC(common side)
- We have established:
- ∠BEC=90∘
- ∠CFB=90∘
- BE=CF
- BC=BC (common side)
- Therefore, by the RHS criterion (Right angle, Hypotenuse, Side), we can conclude:
△BEC≅△CFB
- Hence, we have proved that △BEC is congruent to △CFB.
Topper's Solved these Questions
- CONGRUENCE AND SIMILAR TRIANGLES BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5A
47 Videos
- CONGRUENCE AND SIMILAR TRIANGLES BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5B
8 Videos
- CIRCLE AND ITS TANGENT LINESBOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B
27 Videos
- ELEMENTARY TRIGONOMETRIC IDENTITIES BOOK - LUCENT PUBLICATIONCHAPTER - ELEMENTARY TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE 11B
37 Videos
Similar Questions
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see figure). Show that
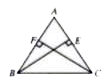
ΔABE≅ΔACF
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
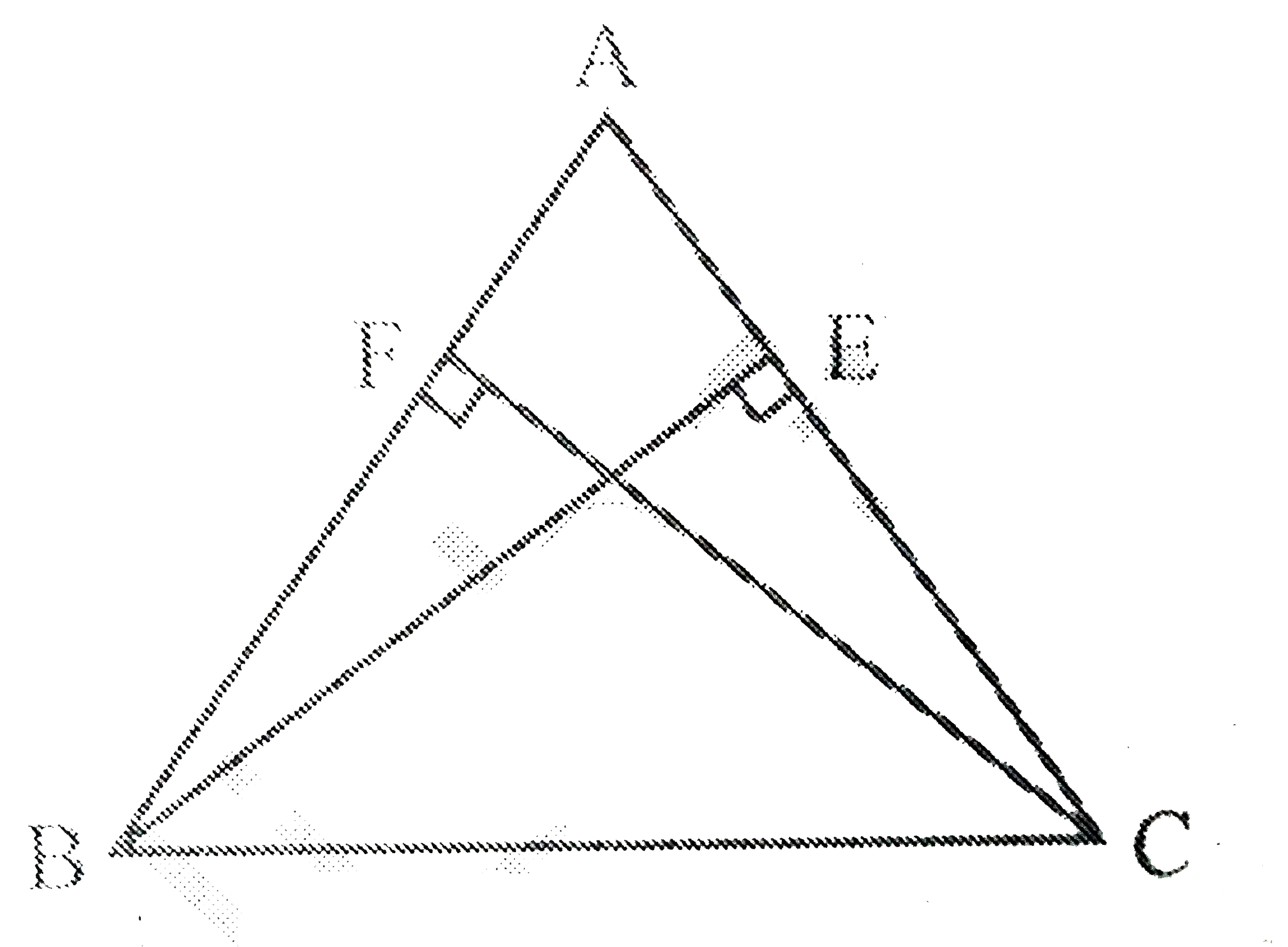
View Solution
Knowledge Check
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.
A∠B=∠CB∠BAE=∠FACC∠AFC=∠AEBDBE = CF
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.

View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see figure). Show that
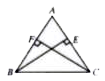
AB=AC, i.e., ABC is an isosceles triangle.
View SolutionABC is a triangle A line is drawn parallel to BC to meet AB and AC in D and E respectively. Prove that the median through A bisects DE.
View SolutionABC is an isosceles triangle in which AB=AC. If D and E are the mid-points of AB and AC respectively, prove that the points B, C, D and E are concyclic.
View SolutionABC is an isosceles triangle in which AB=AC. If DandE are the mid-points of ABandAC respectively, prove that the points B,C,DandE are concylic.
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionThe incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively . Prove that BD = DC.

View Solution
