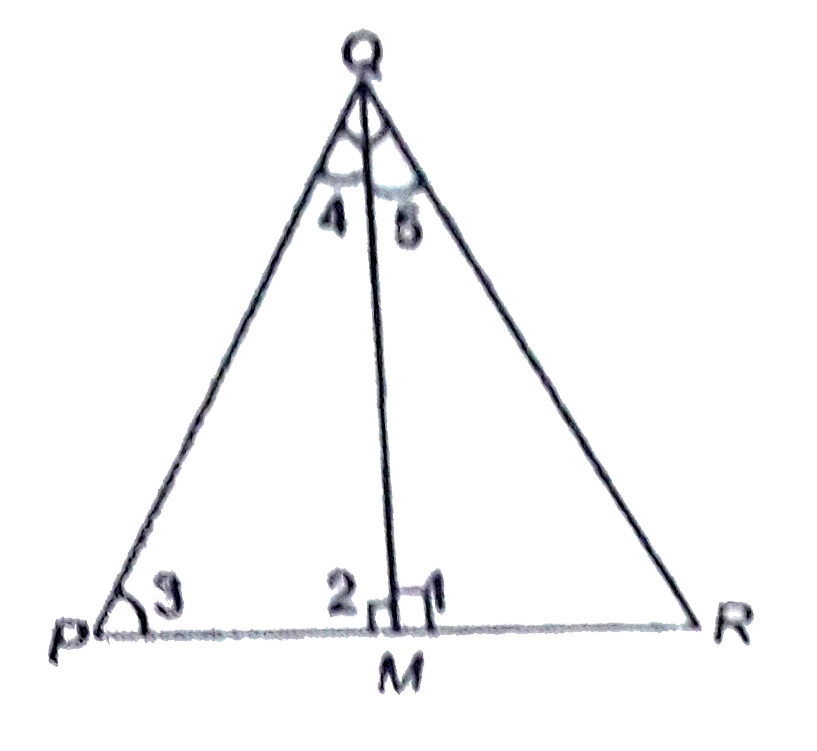
In PQR, QM⊥PR and PR2−PQ2=QR2 . Prove that QM2=PM×MR
Video Solution
Text Solution
since PR2−PQ2=QR2
⇒ PR2=PQ2+QR2
⇒ ∠4+∠5=90∘ ( by the converse of pythagoras theorem)
Now, since , ∠2=90∘
⇒ ∠3+∠4=90∘ (angle sum property) ...(1)
But ∠4+∠5=90∘
From (1) and (2) ,we get
∠3+∠4=∠4+∠5
⇒ ∠3=∠5
Now in △PMQand△QMR
 ( corresponding sides of similar triangle are proportional)
( corresponding sides of similar triangle are proportional)
⇒ QM^(2) = PM xx MR
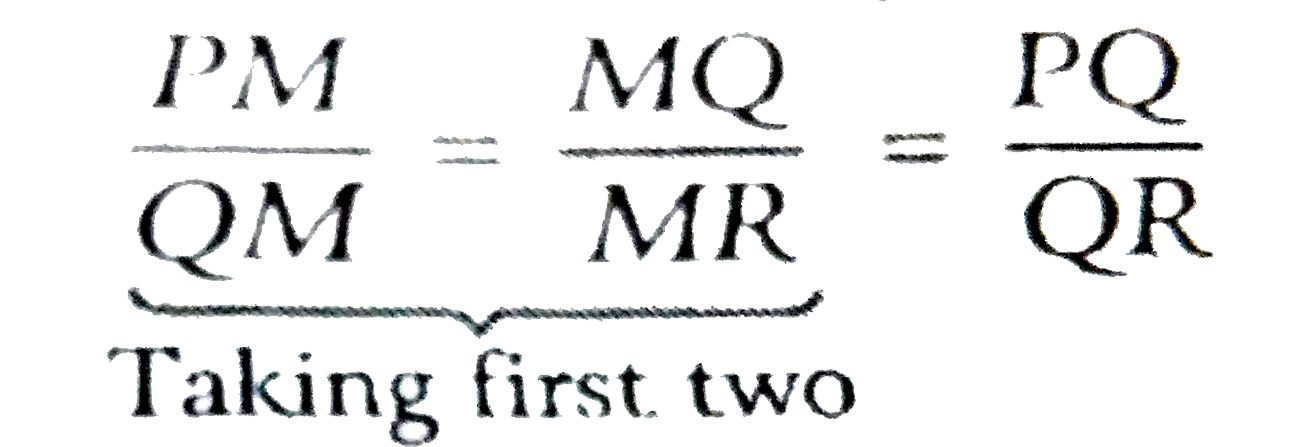
|
Topper's Solved these Questions
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Problems From NCERT/ Exemplar
Explore 14 Videos
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Exercise 6a
Explore 23 Videos
- STATISTICS Book:NAGEEN PRAKASHANChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHANChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Revisions Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
Knowledge Check
If P:Q:R=2:3:4 and P2+Q2+R2=11600,
then find (P+Q−R)A15B16C18D20If P : Q = 2 : 3 and P : R = 4 : 5, then what is (P + Q) : (Q + R)?
A20:27B20:17C10:11D20:29if P:Q:R=2:3:4andP2+Q2+R2=11600, then find P+Q+R, where P,Q and R are whole numbers.
A15B16C18D20
In figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.

View SolutionIn PQR , M and N are points on sides PQ and PR respectively such that PM=15cm and NR=8cm . If PQ=25cm and PR=20cm state whether MNQR .
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.

View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.

View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.

View Solution

