The length of the shadow of a pole inclined at 10∘ to the vertical towards the sun is 2.05 metres, when theelevation of the sun is 38∘. Then, find the length of the pole.
2.05sin42∘sin38∘
2.05sin42∘cos42∘
2.05sin38∘sin42∘
2.05sin42∘sin38∘
Let PO be the tower and OS be its shadow .
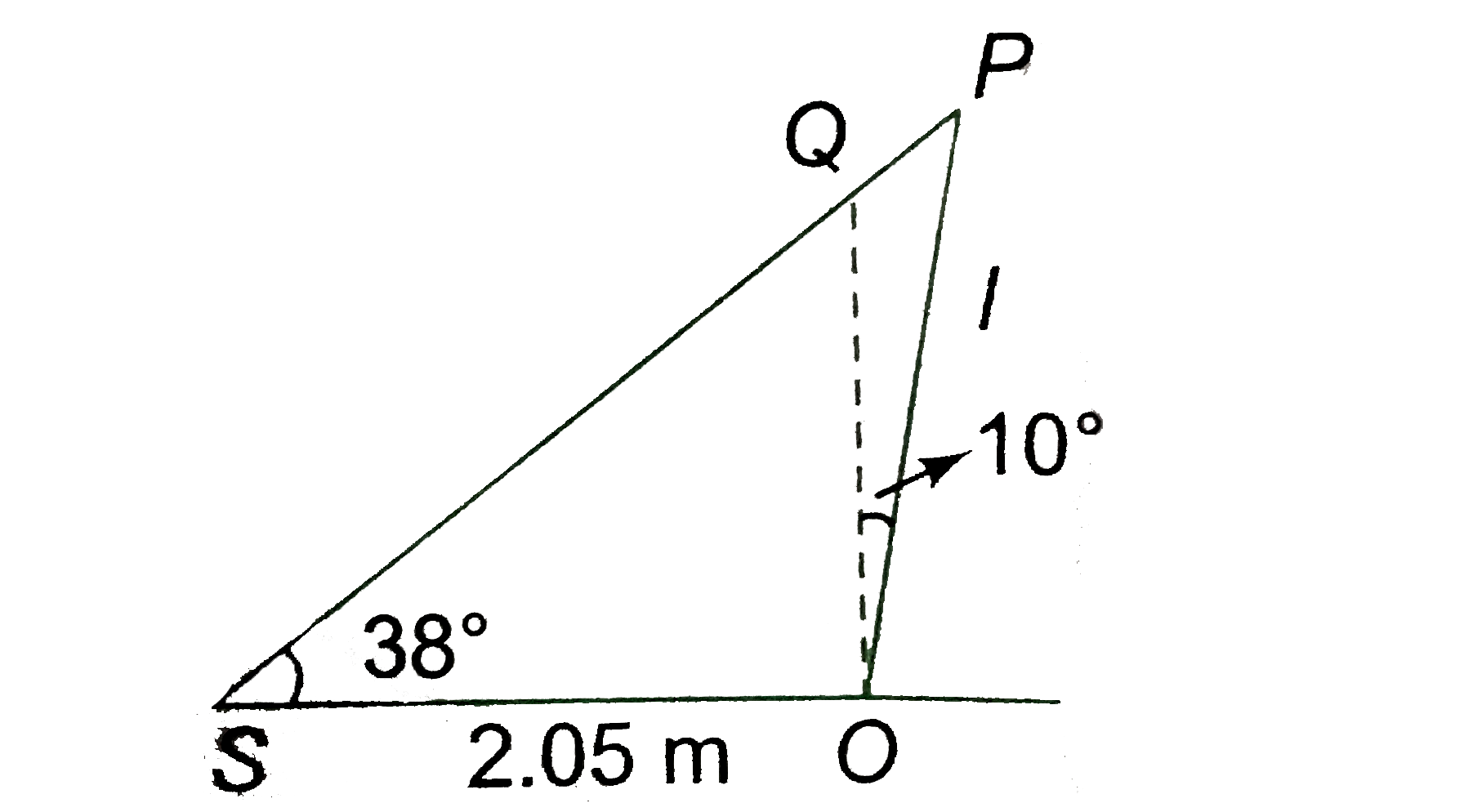
In triangle SOP , using sine rule ,
lsin38∘=2.05sin(∠SPO) ...(1)
∠SPO=180∘−38∘−90∘−10∘=42∘
So from (1), l=2.05sin38∘sin42∘
Topper's Solved these Questions
- HIGHT AND DISTANCE Book:CENGAGEChapter:HIGHT AND DISTANCE Exercise:JEE Previous Year
Explore 3 Videos
- HIGHT AND DISTANCE Book:CENGAGEChapter:HIGHT AND DISTANCE Exercise:JEE Previous Year
Explore 3 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBook:CENGAGEChapter:GRAPHS OF TRIGONOMETRIC FUNCTIONSExercise:Exercise
Explore 22 Videos
- HYPERBOLABook:CENGAGEChapter:HYPERBOLAExercise:JEE Advanced Previous Year
Explore 14 Videos
Similar Questions
Knowledge Check
The length of the shadow of a pole inclined at 10∘ to the vertical towards the sun is 2.05 metres. When the elevation of the sun is 38∘., the length of the pole is
A2.05sin38∘sin42∘B2.05sin42∘sin38∘C2.05cos38∘cos42∘DNone of theseIf the height of a pole is 2√3 metre and the length of its shadow is 2 metre , then the angle of elevation of the sun is
A90∘B45∘C30∘D60∘If the length of shadow of a vertical pole on the horizontal ground is √3 times of its height, then the angles of elevation of sun is :
A15∘B30∘C45∘D60∘
If the height of a pole is 2√3 metres and the length of its shadow is 2 metres, find the angle of elevation of the sun.
View SolutionWhen the shadow of a pole 'h' metres high is √3h3 metres, what is the angle of elevation of the sun at that time ?
View SolutionThe length of the shadow of a tower standing on level ground four to be 2x metres longer when the sun's elevation is 30∘ than where it was 45∘. The height of the tower is
View SolutionThe shadow of a vertical tower becomes 30 metres longer when the altitude of the sun changes from 60∘to45∘ .find the height of the tower .
View SolutionWhat is the angle of elevation of the Sun when the shadow of a pole is √3 times the length of the pole?
View Solution

