A vertical tower stands on a declivity which isinclined at 15∘ to the horizon. From the foot of the tower a man ascends the declivity from 80 feet and then finds that the tower subtends an angle of 30∘. The height of the tower is
40(√6+√2)
20(√6−√2)
40(√6−√2)
80(√6−√2)
Let BC be the declivity and BA be the tower .
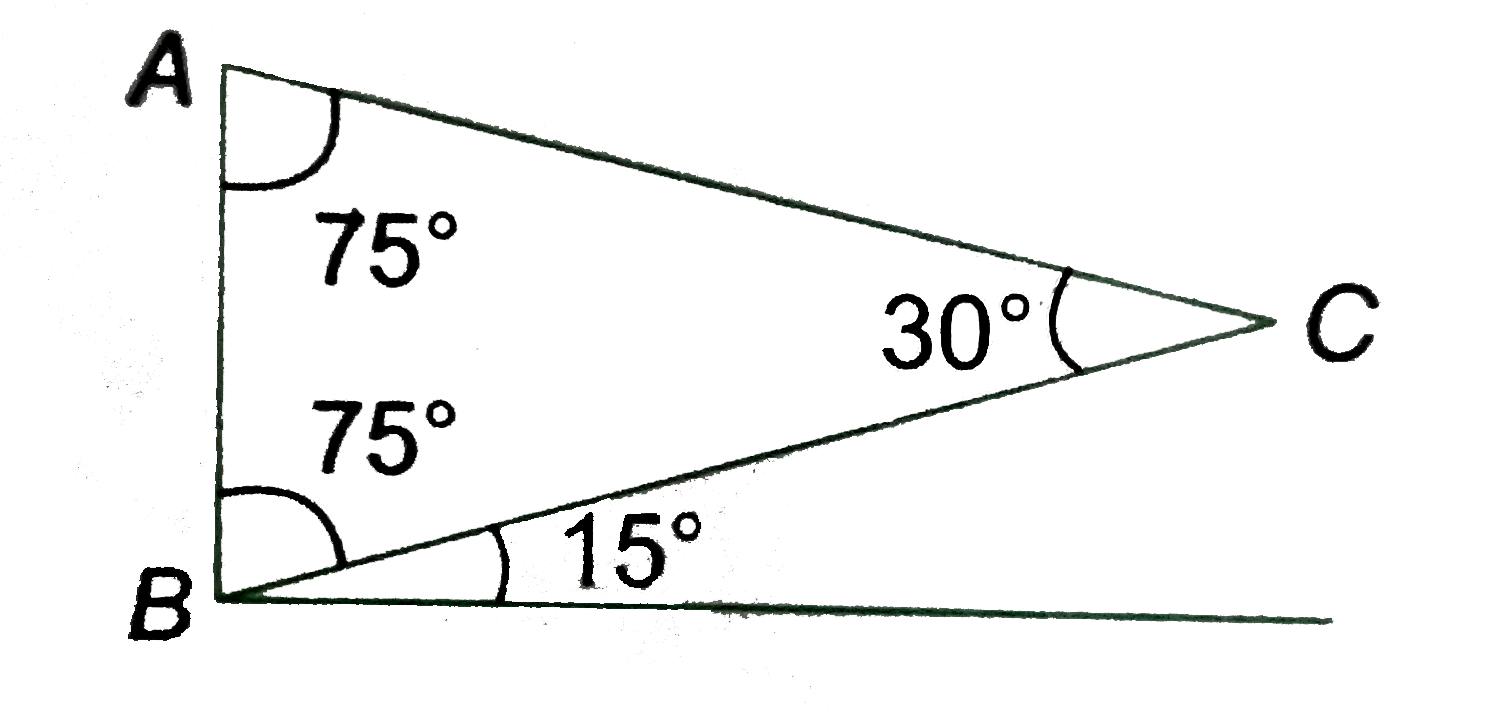
Using sine rule in ΔABC, we get
BCsin75∘=ABsin30∘
⇒AB=80sin30∘sin75∘
⇒AB=40×2√2√3+1=40(√6−√2)
Topper's Solved these Questions
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- HYPERBOLABOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - JEE Advanced Previous Year
14 Videos
Similar Questions
A vertical tower subtends an angle of 60∘ at a point on the same level as the foot of the tower. On moving 100 m further from the first point in line with the tower, it subtends an angle of 30∘ at the point. If the height of the tower is Hm, then the value of H25√3 (in meters) is
View SolutionA vertical tower subtends an angle of 60∘ at a point on the same level as the foot of the tower. On moving 100 m further in line with the tower, it subtends an angle of 30∘ at the point. Then, the height of the tower, it subtends an angle of 30∘ at the point. Then, the height of the tower is
View Solution
Knowledge Check
A vertical tower stands on a declicity which is inclined at 15∘ to the horizon. From the foot of the tower a man ascends the declivity for 80 feet and then finds that the tower substends an angle of 30∘ . The height of the tower is
A40(√6+√2)B20(√6−√2)C40(√6−√2)D80(√6−√2)A vertical tower stands on a declicity which is inclined at 15∘ to the horizon. From the foot of the tower a man ascends the declivity for 80 feet and then finds that the tower substends an angle of 30∘ . The height of the tower is
A20(√6−√2)B40(√6−√2)C40(√6+√2)DNoneA vertical tower stands on a declivity which is inclined at 15∘ to the horizon. From the foot of the tower, a man ascends the declivity from 870 feet an them finds that the tower subtends a angle of 30∘. Then the height of the tower is
A40(√6−√2)B20(√6−√2)C40(√3−√2)DNone of these
A tower stands at the foot of a hill whose inclination to the horizon is 9∘, at a point 40 m up the hill the tower subtends an angle of 54∘. The height of the tower is
View SolutionA tower of height b subtends an angle at a point 0 on the ground level through the foot of the tower and at a distance a from the foot of the tower. A pole mounted on the top of the tower also subtends an equal angle at 0. The height of the pole is
View SolutionA tower standing on a horizontal plane subtends a certain angle at a point 160 m apart from the foot of the tower .On advancing 100 m towards it , the tower is found to subtend an angle twice as be fore .The height of the tower is
View SolutionA tower of height b substends an angle at a point O on the leavel of the foot of the tower and at a distance a from the foot of the tower. If a pole mounted on the lower also subtends an equal angle at O, the height of the pole is
View SolutionA tower standing on a horizontal plane subtends a certain angle at a point 160 m apart from the foot of the tower. On advancing 100 m towards if, the tower is found to subtend an angle twice as before. The height of the tower is -
View Solution