A flagstaff stands in the centre of a rectangular field whose diagonal is 120 m. It subtends angles of 15∘ and 45∘ at the midpoints of the sides of the field. The height of the flagstaff is

A

20m

B

30√2+√3m

C

30√2−√3m

D

40m

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

Let OP be the flagstaff of height 'h' standing at the centre O of the rectengular field ABCD subtending angless 15∘and45∘ at E and F ,respectivily ,
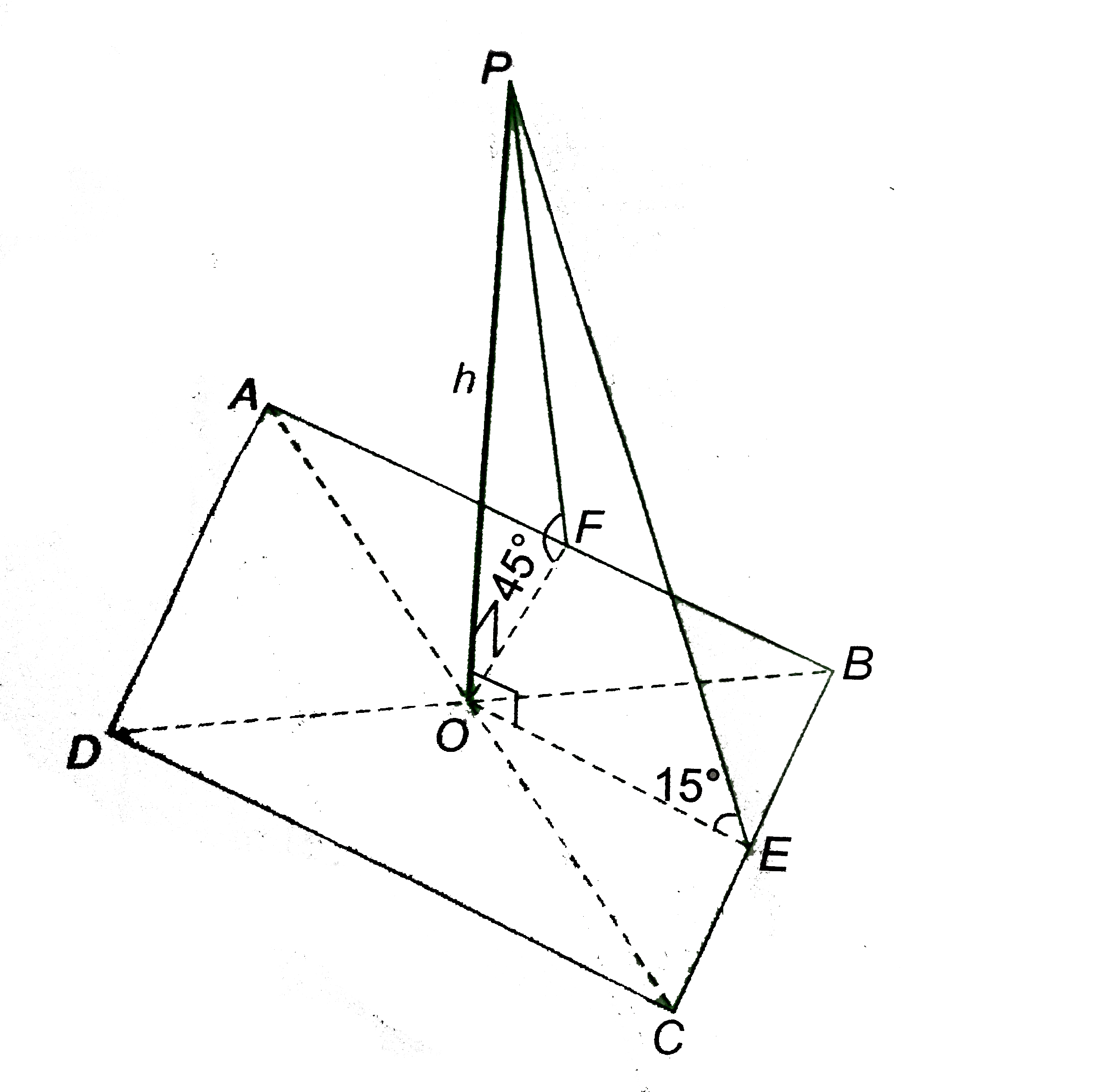
ocr_image
In triangle POE , OE =hcot15∘=h(2+√3)
In triangle POF ,OF = hcot45∘=h
⇒EF=√h2=(2+√3)2h2
2h√2+√3
Triangles ACB and FEB are similar .
so, AC =2EF
⇒120=4h√(2+√3) ,
⇒h=30√2+√3=30√2−√3

Updated on:21/07/2023
|
Class 12MATHSHIGHT AND DISTANCE

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A flagstaff stands in the centre of a rectangular field whose diagonal is 1200 m and subtends angle 15∘ and 45∘ at the mid points of the sides of the field. The height of the flagstaff is

    A200m
    B300√2+√3m
    C300√2−√3m
    D400 m

  • A pole stands at the centre of a rectangular field and it subtends angles of 15∘and45∘ at the mid-points of the sides of the field. If the length of its diagonal is 1200 m, then the height of the flag staff is

    A400 m
    B200 m
    C300√2−√3m
    D300√2−√3)m

  • One side of a rectangular field is 9 m and one of its diagonal is 20 m. Find the area of the field.

    A9√319sqm
    B7√319sqm
    C2√319sqm
    D5√319sqm