From the bottom of a pole of height h, the angle of elevation of the top of a tower is α. The pole subtends an angle β at the top of the tower. find the height of the tower.
hcot(α−β)cot(α−β)−cotα
htan(α−β)tan(α−β)−tanα
cot(α−β)cot(α−β)−cotα
None of these
Let AB be the tower of height H and CD be the pole
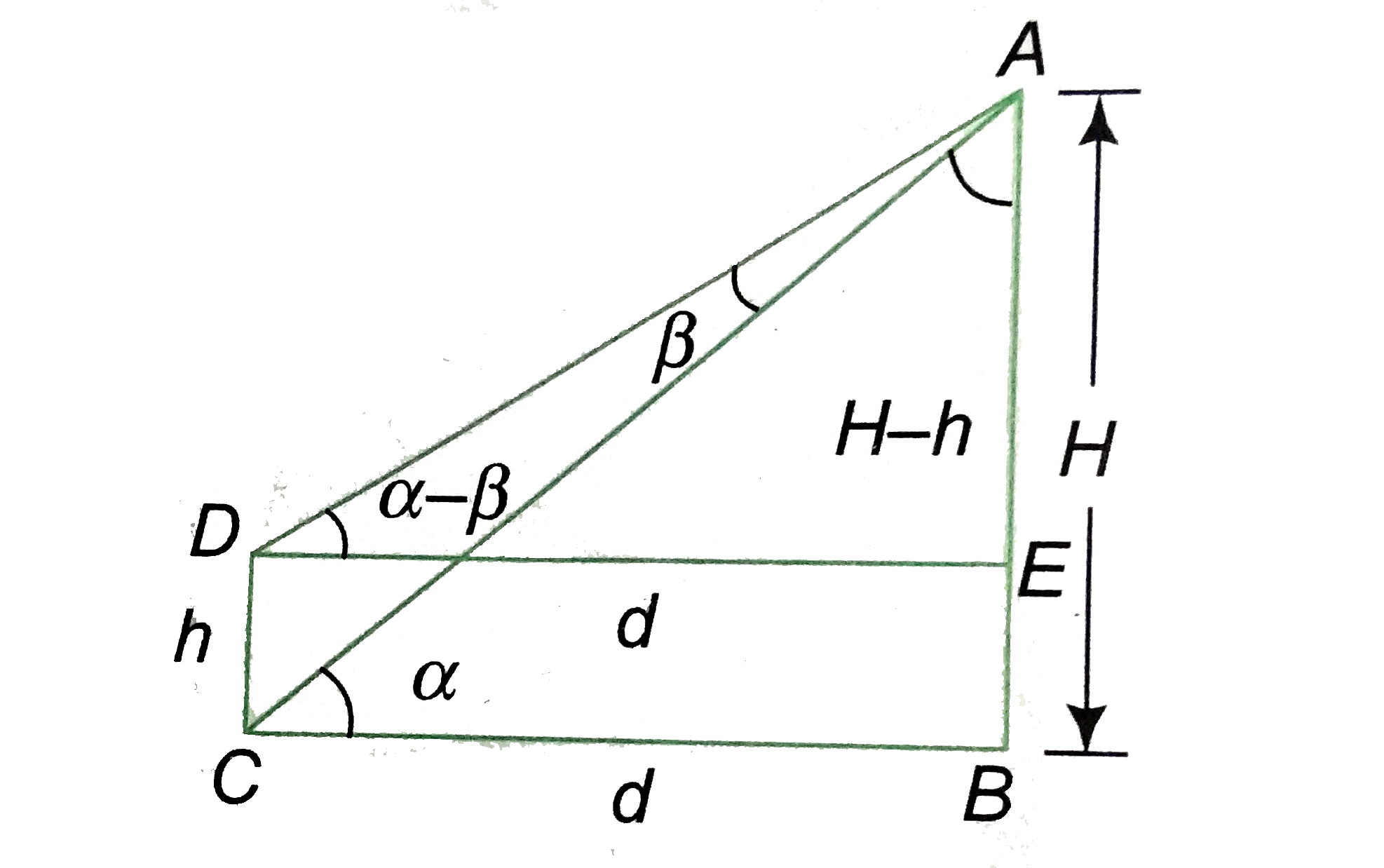
In triangle ABC, d =hcotα
In triangle AED,d =(H−h)cot(α−β)
⇒Hcotα=(H−h)cot(α−β)
∴H=hcot(α−β)cot(α−β)−cotα
Topper's Solved these Questions
- HIGHT AND DISTANCE Book:CENGAGEChapter:HIGHT AND DISTANCE Exercise:JEE Previous Year
Explore 3 Videos
- HIGHT AND DISTANCE Book:CENGAGEChapter:HIGHT AND DISTANCE Exercise:JEE Previous Year
Explore 3 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBook:CENGAGEChapter:GRAPHS OF TRIGONOMETRIC FUNCTIONSExercise:Exercise
Explore 22 Videos
- HYPERBOLABook:CENGAGEChapter:HYPERBOLAExercise:JEE Advanced Previous Year
Explore 14 Videos
Similar Questions
From the top of a pole of height h, the angle of elevation of the top of the tower is α. The pole subtends an angle β at the top of the tower. The height of the tower is____
View SolutionFrom the bottom of a pole of height h, the angle of elevation of the top of the tower is α. The pole subtends an angle β at the top of the tower. Prove that the height of the tower is h sinα cosec βcos(α−β)
View Solution
Knowledge Check
Choose the most appropriate options.
From the bottom of a pole of height h, the angle of elevation of the top of a tower is α The pole subtends an angle β at the top of tower. The height of the tower isAhsinαsin(α−β)sinβBhsinαcos(α+β)cosβChsinαcos(α−β)sinβDhsinαsin(α+β)cosβFrom the top of the house 18m high, if the angle of elevation of the top of a tower is 45° and the angle of depression of the foot of the tower is 30°, then the height of the tower is
A18√3 mB18(√3+1) mC18(√3−1)mD6√3m
The angle of elevation of the top of a tower at a point on the ground, 50 m away from the foot of the tower, is 60°. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30∘. Find the height of the tower.
View SolutionFrom the top of a cliff 15mt height, the angle of elevation of the top of a tower is found to be equal to the angle of depression of the foot of the tower.The height of the tower is
View SolutionFrom the top of a 7 m high building, the angle of elevation of the top of a tower is 60° and the angle of depression of the foot of the tower is 30°. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30m away from the foot of the tower, is 30∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground which is 30 m away from the foot of the tower is 30∘. Find the height of the tower.
View Solution