The shadow of a vertical tower becomes 30 metres longer when the altitude of the sun changes from 60∘to45∘ .find the height of the tower .
15√3 metres
15(3+√3) metres
15(3−√3) metres
12(3+√3) metres
The correct Answer is:B
To solve the problem, we need to find the height of the tower based on the information given about the shadow lengths at different angles of elevation of the sun.
Step 1: Define Variables
Let h be the height of the tower in meters.
Step 2: Use Trigonometry for the First Angle
When the angle of elevation of the sun is 60∘, we can use the tangent function:
tan(60∘)=hs1
where s1 is the length of the shadow when the angle is 60∘. We know that:
tan(60∘)=√3
Thus, we have:
√3=hs1⟹s1=h√3
Step 3: Use Trigonometry for the Second Angle
When the angle of elevation of the sun changes to 45∘, we can again use the tangent function:
tan(45∘)=hs2
where s2 is the length of the shadow when the angle is 45∘. We know that:
tan(45∘)=1
Thus, we have:
1=hs2⟹s2=h
Step 4: Set Up the Equation
According to the problem, the shadow becomes 30 meters longer when the angle changes from 60∘ to 45∘. Therefore, we can write:
s2=s1+30
Substituting the expressions for s1 and s2:
h=h√3+30
Step 5: Solve for h
To eliminate the fraction, we can multiply the entire equation by √3:
√3h=h+30√3
Now, rearranging the equation gives:
√3h−h=30√3
Factoring out h:
h(√3−1)=30√3
Now, we can solve for h:
h=30√3√3−1
Step 6: Rationalize the Denominator
To simplify further, we can multiply the numerator and denominator by √3+1:
h=30√3(√3+1)(√3−1)(√3+1)=30√3(√3+1)3−1=30√3(√3+1)2
This simplifies to:
h=15√3(√3+1)=15(3+√3)=45+15√3
Final Answer
Thus, the height of the tower is:
h=45+15√3 meters
Let h be the height of the tower in meters.
When the angle of elevation of the sun is 60∘, we can use the tangent function:
tan(60∘)=hs1
where s1 is the length of the shadow when the angle is 60∘. We know that:
tan(60∘)=√3
Thus, we have:
√3=hs1⟹s1=h√3
When the angle of elevation of the sun changes to 45∘, we can again use the tangent function:
tan(45∘)=hs2
where s2 is the length of the shadow when the angle is 45∘. We know that:
tan(45∘)=1
Thus, we have:
1=hs2⟹s2=h
According to the problem, the shadow becomes 30 meters longer when the angle changes from 60∘ to 45∘. Therefore, we can write:
s2=s1+30
Substituting the expressions for s1 and s2:
h=h√3+30
To eliminate the fraction, we can multiply the entire equation by √3:
√3h=h+30√3
Now, rearranging the equation gives:
√3h−h=30√3
Factoring out h:
h(√3−1)=30√3
Now, we can solve for h:
h=30√3√3−1
To simplify further, we can multiply the numerator and denominator by √3+1:
h=30√3(√3+1)(√3−1)(√3+1)=30√3(√3+1)3−1=30√3(√3+1)2
This simplifies to:
h=15√3(√3+1)=15(3+√3)=45+15√3
Thus, the height of the tower is:
h=45+15√3 meters
Topper's Solved these Questions
Similar Questions
The shadow of a tower is found to be x metre longer, when the angle of elevation of the sun changes from 60∘ to 45∘. If the height of the tower is 5(3+√3)m, then what is x equal to ?
View SolutionThe shadow of a vertical tower on level ground increases by 10 m when the altitude of the sun changes from 45∘ to 30∘. Find the height of the tower.
View Solution
Knowledge Check
The shadow of a tower standing on a level plane is found to be 40 m longer when the sun 's altitude is 45∘ , than when it is 60∘ . The height of the tower is
A644 mB66.644 mC54.644 mD76.644 mThe shadow of a tower is found to be 60 ft. longer when the sun's altitude has become 60∘ from 30∘. The height of the tower from the ground is
A350 ft. app.B400 ft. app.C51 ft. app.DNoneThe shadow of a tower on ground level is increased by 30 m, when the angle of depression by the sun changes from 60∘ to 30∘. The height of the tower is?
A. 12√3 m
B. 17√3 m
C. 16√3m
D. 15√3 mABBCCDDA
The length of the shadow of the vertical tower on level ground increases by 10m when the altitude of the sun changes from 45∘ to 30∘.The height of the tower is:
समतल भूमि पर खड़ी मीनार की छाया की लंबाई 10 मीटर तक बढ़ जाती है जब सूर्य की ऊँचाई 45∘ से 30∘ तक बदल जाती है। टॉवर की ऊंचाई है:
View SolutionThe shadow of a vertical tower on level ground increases by 10 metres, when the altitude of the sun changes from angle of elevatin 450→300. Find the height of the tower, correct to one place of decimal. (Take√3=1.73
View SolutionThe shadow of a tower standing on a level ground is found to be 20 m longer when the sun's altitude is 45∘ than when it is 60∘ .Find the height of the tower .
View SolutionThe shadow of a tower standing in a level plane is found to be 18 m shorter when the sun's altitude changes from 30∘ to 45∘. Show that the height of the tower is 9(1+√3)m.
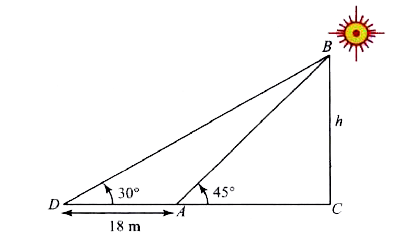
View SolutionThe shadow of a tower standing on a level ground is found to be 60 metres longer when the sun's altitude is 30∘ than when it is 45∘. The height of the tower is____
View Solution
