The shadow of a vertical tower on level ground increases by 10 metres, when the altitude of the sun changes from angle of elevatin 450→300. Find the height of the tower, correct to one place of decimal. (Take√3=1.73
To solve the problem, we need to find the height of the tower based on the change in the shadow length when the angle of elevation of the sun changes from 45∘ to 30∘.
Step 1: Understand the problem
We have a vertical tower, and we know that when the angle of elevation of the sun changes from 45∘ to 30∘, the shadow of the tower increases by 10 meters. We need to find the height of the tower.
Step 2: Set up the equations
Let h be the height of the tower and x be the length of the shadow when the angle of elevation is 30∘.
From trigonometry, we know:
- When the angle of elevation is 45∘:
tan(45∘)=hx−10⟹1=hx−10⟹h=x−10
- When the angle of elevation is 30∘:
tan(30∘)=hx⟹1√3=hx⟹h=x√3
Step 3: Set the equations equal to each other
Now we have two expressions for h:
1. h=x−10
2. h=x√3
Setting them equal gives:
x−10=x√3
Step 4: Solve for x
To solve for x, we can multiply both sides by √3 to eliminate the fraction:
√3(x−10)=x
√3x−10√3=x
Rearranging gives:
√3x−x=10√3
(√3−1)x=10√3
x=10√3√3−1
Step 5: Rationalize the denominator
To simplify x, we multiply the numerator and denominator by √3+1:
x=10√3(√3+1)(√3−1)(√3+1)=10√3(√3+1)3−1=10√3(√3+1)2
x=5√3(√3+1)=5(3+√3)=15+5√3
Step 6: Substitute x back to find h
Now we can substitute x back into one of the equations for h:
h=x−10=(15+5√3)−10=5+5√3
Step 7: Calculate h
Using the approximation √3≈1.73:
h=5+5(1.73)=5+8.65=13.65
Step 8: Round to one decimal place
Thus, the height of the tower, rounded to one decimal place, is:
13.7 meters
We have a vertical tower, and we know that when the angle of elevation of the sun changes from 45∘ to 30∘, the shadow of the tower increases by 10 meters. We need to find the height of the tower.
Let h be the height of the tower and x be the length of the shadow when the angle of elevation is 30∘.
- When the angle of elevation is 45∘:
tan(45∘)=hx−10⟹1=hx−10⟹h=x−10
tan(30∘)=hx⟹1√3=hx⟹h=x√3
Now we have two expressions for h:
1. h=x−10
2. h=x√3
x−10=x√3
To solve for x, we can multiply both sides by √3 to eliminate the fraction:
√3(x−10)=x
√3x−10√3=x
Rearranging gives:
√3x−x=10√3
(√3−1)x=10√3
x=10√3√3−1
To simplify x, we multiply the numerator and denominator by √3+1:
x=10√3(√3+1)(√3−1)(√3+1)=10√3(√3+1)3−1=10√3(√3+1)2
x=5√3(√3+1)=5(3+√3)=15+5√3
Now we can substitute x back into one of the equations for h:
h=x−10=(15+5√3)−10=5+5√3
Using the approximation √3≈1.73:
h=5+5(1.73)=5+8.65=13.65
Thus, the height of the tower, rounded to one decimal place, is:
13.7 meters
Topper's Solved these Questions
Similar Questions
The shadow of a vertical tower on level ground increases by 10 metres, when the altitude of the sun changes from angle of elevatin 450→300. Find the height of the tower, correct to one place of decimal. (Take√3=1.73
View SolutionThe shadow of a vertical tower on level ground increases by 10 m when the altitude of the sun changes from 45∘ to 30∘. Find the height of the tower.
View Solution
Knowledge Check
The shadow of a vertical tower becomes 30 metres longer when the altitude of the sun changes from 60∘to45∘ .find the height of the tower .
A15√3 metresB15(3+√3) metresC15(3−√3) metresD12(3+√3) metresThe shadow of a tower standing on a level plane is found to be 40 m longer when the sun 's altitude is 45∘ , than when it is 60∘ . The height of the tower is
A644 mB66.644 mC54.644 mD76.644 m
The length of the shadow of the vertical tower on level ground increases by 10m when the altitude of the sun changes from 45∘ to 30∘.The height of the tower is:
समतल भूमि पर खड़ी मीनार की छाया की लंबाई 10 मीटर तक बढ़ जाती है जब सूर्य की ऊँचाई 45∘ से 30∘ तक बदल जाती है। टॉवर की ऊंचाई है:
View SolutionThe shadow of a tower,when the angle of elevation of the sum is 45∘ , is found to be 10metres longer than when the angle of elevation, when 60∘. Find the height of the tower.
View SolutionThe shadow of a tower standing on a level ground is found to be 60 metres longer when the sun's altitude is 30∘ than when it is 45∘. The height of the tower is____
View SolutionThe shadow of a tower standing on a level ground is found to be 20 m longer when the sun's altitude is 45∘ than when it is 60∘ .Find the height of the tower .
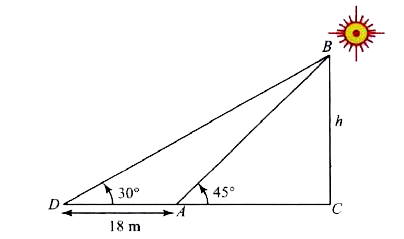
View SolutionThe shadow of a tower standing in a level plane is found to be 18 m shorter when the sun's altitude changes from 30∘ to 45∘. Show that the height of the tower is 9(1+√3)m.
View SolutionThe shadow of a tower is found to be x metre longer, when the angle of elevation of the sun changes from 60∘ to 45∘. If the height of the tower is 5(3+√3)m, then what is x equal to ?
View Solution
