The shadow of a vertical tower on level ground increases by 10 m when the altitude of the sun changes from 45∘ to 30∘. Find the height of the tower.
The correct Answer is:13.65 m
To find the height of the tower, we can use the information given about the angles of elevation and the change in the length of the shadow. Let's break down the solution step by step.
Step 1: Define the Variables
Let:
- y = height of the tower
- x = length of the shadow when the angle of elevation is 45∘
Step 2: Use the Tangent Function for the First Angle
For the angle of elevation of 45∘:
tan(45∘)=height of towerlength of shadow=yx
Since tan(45∘)=1:
1=yx⟹y=x(Equation 1)
Step 3: Use the Tangent Function for the Second Angle
When the angle of elevation changes to 30∘, the length of the shadow increases by 10 m, so the new length of the shadow is x+10:
tan(30∘)=yx+10
Since tan(30∘)=1√3:
1√3=yx+10
Cross-multiplying gives:
y=1√3(x+10)(Equation 2)
Step 4: Substitute Equation 1 into Equation 2
From Equation 1, we have y=x. Substitute y in Equation 2:
x=1√3(x+10)
Step 5: Solve for x
Multiply both sides by √3 to eliminate the fraction:
√3x=x+10
Rearranging gives:
√3x−x=10
(√3−1)x=10
x=10√3−1
Step 6: Find y
Using Equation 1, y=x:
y=10√3−1
Step 7: Rationalize the Denominator
To simplify y:
y=10(√3+1)(√3−1)(√3+1)=10(√3+1)3−1=10(√3+1)2=5(√3+1)
Final Answer
Thus, the height of the tower is:
y=5(√3+1) meters
Let:
- y = height of the tower
- x = length of the shadow when the angle of elevation is 45∘
For the angle of elevation of 45∘:
tan(45∘)=height of towerlength of shadow=yx
Since tan(45∘)=1:
1=yx⟹y=x(Equation 1)
When the angle of elevation changes to 30∘, the length of the shadow increases by 10 m, so the new length of the shadow is x+10:
tan(30∘)=yx+10
Since tan(30∘)=1√3:
1√3=yx+10
Cross-multiplying gives:
y=1√3(x+10)(Equation 2)
From Equation 1, we have y=x. Substitute y in Equation 2:
x=1√3(x+10)
Multiply both sides by √3 to eliminate the fraction:
√3x=x+10
Rearranging gives:
√3x−x=10
(√3−1)x=10
x=10√3−1
Using Equation 1, y=x:
y=10√3−1
To simplify y:
y=10(√3+1)(√3−1)(√3+1)=10(√3+1)3−1=10(√3+1)2=5(√3+1)
Thus, the height of the tower is:
y=5(√3+1) meters
Topper's Solved these Questions
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - LONG ANSWER TYPE QUESTIONS
19 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - PRACTICE-TEST (SECTION-A)
4 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - PRACTICE-TEST (SECTION-D)
1 Video
- REAL NUMBERSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - REAL NUMBERSEXERCISE - LONG ANSWER TYPE QUESTION
15 Videos
- STATISTICSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - Practice -Test
5 Videos
Similar Questions
The length of the shadow of the vertical tower on level ground increases by 10m when the altitude of the sun changes from 45∘ to 30∘.The height of the tower is:
समतल भूमि पर खड़ी मीनार की छाया की लंबाई 10 मीटर तक बढ़ जाती है जब सूर्य की ऊँचाई 45∘ से 30∘ तक बदल जाती है। टॉवर की ऊंचाई है:
View SolutionThe shadow of a vertical tower on level ground increases by 10 metres, when the altitude of the sun changes from angle of elevatin 450→300. Find the height of the tower, correct to one place of decimal. (Take√3=1.73
View Solution
Knowledge Check
The shadow of a tower on ground level is increased by 30 m, when the angle of depression by the sun changes from 60∘ to 30∘. The height of the tower is?
A. 12√3 m
B. 17√3 m
C. 16√3m
D. 15√3 mABBCCDDAThe shadow of a vertical tower becomes 30 metres longer when the altitude of the sun changes from 60∘to45∘ .find the height of the tower .
A15√3 metresB15(3+√3) metresC15(3−√3) metresD12(3+√3) metresThe shadow of a tower standing on a level plane is found to be 40 m longer when the sun 's altitude is 45∘ , than when it is 60∘ . The height of the tower is
A644 mB66.644 mC54.644 mD76.644 m
The shadow of a tower is found to be x metre longer, when the angle of elevation of the sun changes from 60∘ to 45∘. If the height of the tower is 5(3+√3)m, then what is x equal to ?
View SolutionThe shadow of a tower standing on a level ground is found to be 20 m longer when the sun's altitude is 45∘ than when it is 60∘ .Find the height of the tower .
View SolutionThe shadow of a tower standing in a level plane is found to be 18 m shorter when the sun's altitude changes from 30∘ to 45∘. Show that the height of the tower is 9(1+√3)m.
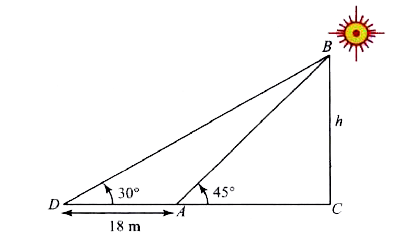
View SolutionThe shadow of a tower standing on a level ground is found to be 40 m longer when the Suns altitude is 30othan when it is 60o. Find the height of the tower.
View SolutionThe shadow of a tower standing on a level ground is found to be 40m longer when Suns altitude is 30o than when it was 60o . Find the height of the tower.
View Solution
