If tanθ=x−yx+y,then value of sinθ is eqaul to (If 0∘≤θ≤90∘)
x−y√2(x2+y2)
x+y√2(x2+y2)
x+y√2(x2−y2)
x−y√2(x2−y2)
The correct Answer is:A
To find the value of sinθ given that tanθ=x−yx+y, we can follow these steps:
Step 1: Understand the relationship between sine, cosine, and tangent
We know that:
tanθ=sinθcosθ
From the given equation, we can express sinθ in terms of tanθ and cosθ.
Step 2: Set up the right triangle
We can visualize tanθ as the ratio of the opposite side (perpendicular) to the adjacent side (base) of a right triangle:
- Let the opposite side (perpendicular) be x−y.
- Let the adjacent side (base) be x+y.
Step 3: Calculate the hypotenuse
Using the Pythagorean theorem, the hypotenuse h can be calculated as:
h=√(x−y)2+(x+y)2
Now, we will expand this expression:
h=√(x−y)2+(x+y)2=√(x2−2xy+y2)+(x2+2xy+y2)=√2x2+2y2
This simplifies to:
h=√2(x2+y2)
Step 4: Calculate sinθ
Now, we can find sinθ using the definition:
sinθ=oppositehypotenuse=x−y√2(x2+y2)
Final Result
Thus, the value of sinθ is:
sinθ=x−y√2(x2+y2)
We know that:
tanθ=sinθcosθ
From the given equation, we can express sinθ in terms of tanθ and cosθ.
We can visualize tanθ as the ratio of the opposite side (perpendicular) to the adjacent side (base) of a right triangle:
- Let the opposite side (perpendicular) be x−y.
- Let the adjacent side (base) be x+y.
Using the Pythagorean theorem, the hypotenuse h can be calculated as:
h=√(x−y)2+(x+y)2
Now, we will expand this expression:
h=√(x−y)2+(x+y)2=√(x2−2xy+y2)+(x2+2xy+y2)=√2x2+2y2
This simplifies to:
h=√2(x2+y2)
Now, we can find sinθ using the definition:
sinθ=oppositehypotenuse=x−y√2(x2+y2)
Thus, the value of sinθ is:
sinθ=x−y√2(x2+y2)
Topper's Solved these Questions
Similar Questions
Knowledge Check
If sin2θ=√32 then the value of sin3θ is equal to (Take 0∘≤θ≤90∘)
A12B1C0D√32If cosθ=x2−y2x2+y2 then the value of cotθ is equal to (If 0≤θ≤90∘)
A2xyx2−y2B2xyx2+y2Cx2+y22xyDx2−y22xyIf
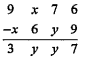
then value of x and y are eqaul toAx=9,y=3Bx=3,y=9Cx=5,y=8Dx=4,y=8
