If <x1<x2<x3<π, then prove that sin(x1+x2+x33)<sinx1+sinx2+sinx33 . Hence or otherwise prove that if A.B.C are angles of a triangle, then the maximum value of sinA+sinB+sinC is 3√32
Draw the graph of y = sin x. 0<x<π and take points A(x1,sinx1),B(x2,sinx2) and C(x3,sinx3).
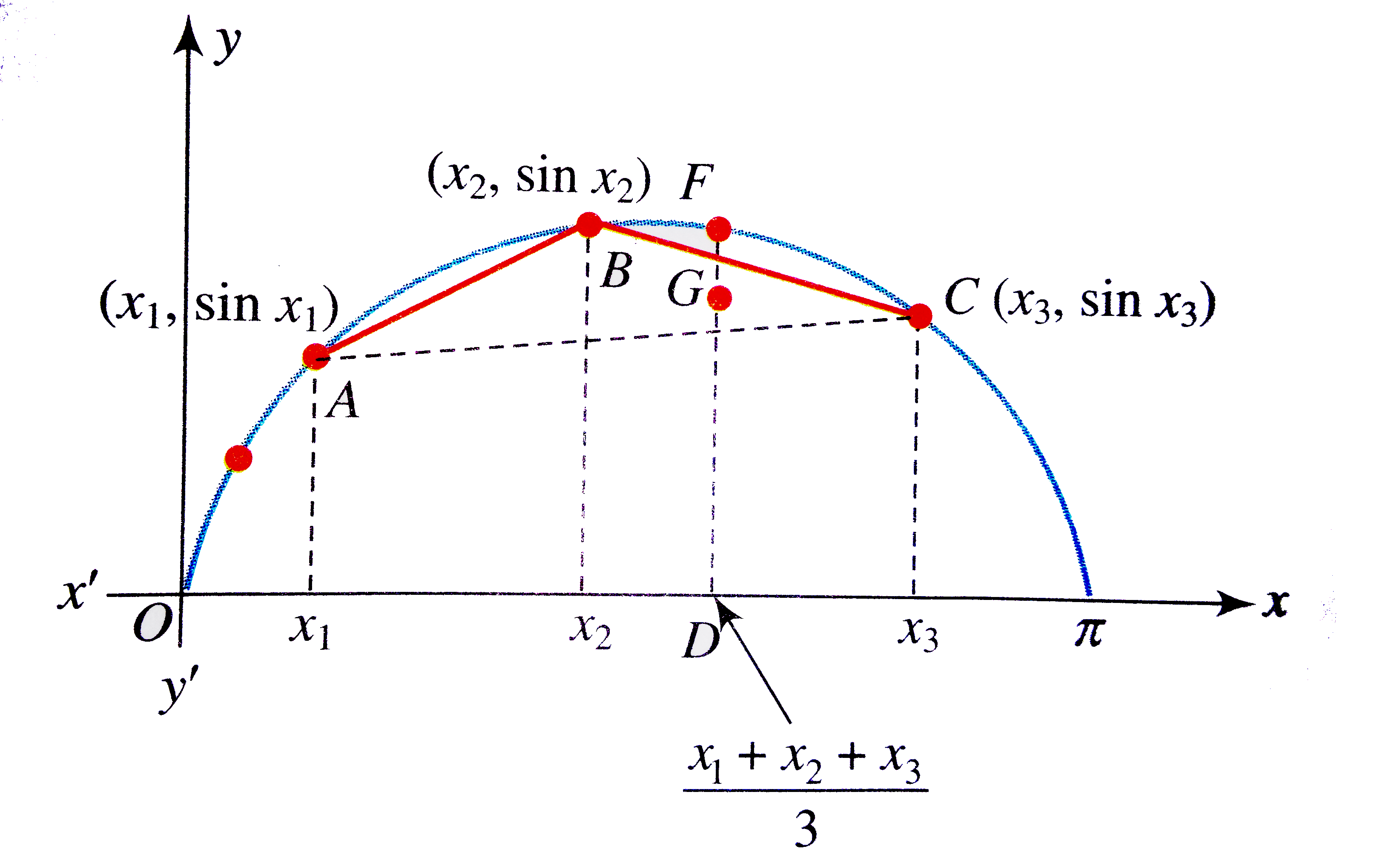
Let the points A, B, C form a traingle.
y - coordinate of the centroid G is sinx1+sinx2+sinx33
and y - coordinate of the point f is sin(x1+x2+x33) (as abscissa of F is x1+x2+x33)
From the diagram, FD>GD.
Hence sin(x1+x2+x33)>sinx1+sinx2+sinx33
If A+B+C=π, then
sin(A+B+C3)>sinA+sinB+sinC3
⇒ sinπ3>sinA+sinB+sinC3
⇒ 3√32>sinA+sinB+sinC
⇒ maximum value of (sinA+sinB+sinC)=3√32
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
Similar Questions
Draw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionDraw the graph of y=1(1/x).
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionIf (xi,1xi),i=1,2,3,4 are four distinct points on a circle, then (A) x1x2=x3x4 (B) x1x2x3x4=1 (C) x1+x2+x3+x4=1 (D) 1x1+1x2+1x3+1x4=1
View SolutionIf xi>0 for 1≤i≤n and x1+x2+x3+…+xn=π then the greatest value of the sum sinx1+sinx2+sinx3+…+sinn=… (A) n (B) π (C) nsin πn (D) none of these
View Solutionसिद्ध कीजिये की बिंदु (x1,y1),(x2,y2) तथा (x3,y3) शीर्ष वाले त्रिभुज के केन्द्रक के निर्देशांक (x1+x2+x33,y1+y2+y33) है| यह भी सिद्ध कीजिये की मध्यमिकाएँ संगामि है|
View SolutionIF A=[−1342],B=[213−5],X=[x1x2x3x4] and A+B=X, the find the values of x1,x2,x3,x4.
View SolutionLet ϕ1(x)=x+a2,ϕ2(x)=x2+b1x+b2,x1=2,x2=3 and x3=5 and Δ=∣∣ ∣ ∣∣111ϕ1(x1)ϕ1(x2)ϕ1(x3)ϕ2(x1)ϕ2(x2)ϕ2(x3)∣∣ ∣ ∣∣ . Find the value of Δ.
View SolutionA=[−1342],B=[213−5] మరియు X=[x1x2x3x4],A+B=X అయితే x1,x2,x3,x4 ల విలువలు కనుక్కోండి.
View SolutionA triangle has vertices Ai(xi,yi)fori=1,2,3 If the orthocentre of triangle is (0,0), then prove that
∣x2−x3y2−y3y1(y2−y3)+x1(x2−x3)
x3−x1y2−y3y2(y3−y1)+x1(x3−x1)
x1−x2y2−y3y3(y1−y2)+x1(x1−x2)∣=0
View SolutionIf 0<x1<x2<x3<π, then prove that sin(x1+x2+x33)<sinx1+sinx2+sinx33 . Hence or otherwise prove that if A,B,C are angles of a triangle, then the maximum value of sinA+sinB+sinC is 3√32
View SolutionIf the join of (x1,y1) and (x2,y2) makes on obtuse angle at (x3,y3), then prove that (x3−x1)(x3−x2)+(y3−y1)(y3−y2)<0
View Solutionprove that if the variance of the observations x1,x2,x3,…….,xn is σ2 then the variance of x1+a,x2+a,x3+a,…………..,xn+a is σ2 .
View SolutionProve that the points : (x1,y1),(x2,y2),(x3,y3)
are collinear if ⎡⎢⎣x1y11x2y21x3y31⎤⎥⎦=0
View SolutionGiven the sequence of numbers x1,x2,x3,...x1005. which satisfy x1x1+1=x2x2+3=x3x3+5=...=x1005x1005+2009. Also, x1+x2+...x1005=2010. Nature of the sequence is
View SolutionIf A(x1,y1),B(x2,y2) and C(x3,y3) are vertices of an equilateral triangle whose each side is equal to 'a', then prove that, ∣∣ ∣ ∣∣x1y12x2y22x3y32∣∣ ∣ ∣∣2=3a4
View Solution
