Solve $sin x ≻ \frac{1}{2} or$ find the domain of $f (x) = \frac{1}{\sqrt{1 + 2 sin x}}$

Video Solution

Text Solution

Verified by Experts

For f(x) to get defined, we must have 1 + 2 sin $x > 0$ or $sin x > - \frac{1}{2}$
As the function sin x has fundamental period $2 π$ , it is sufficient to solve the inequality first on the interval of length $2 π$ , and then get the solution set by adding numbers of the form $2 n π, n \in Z$ , to each of the solutions obtained on that interval.
Thus, let us solve this inequality on the interval $[- \frac{π}{2}, \frac{3 π}{2}]$ .

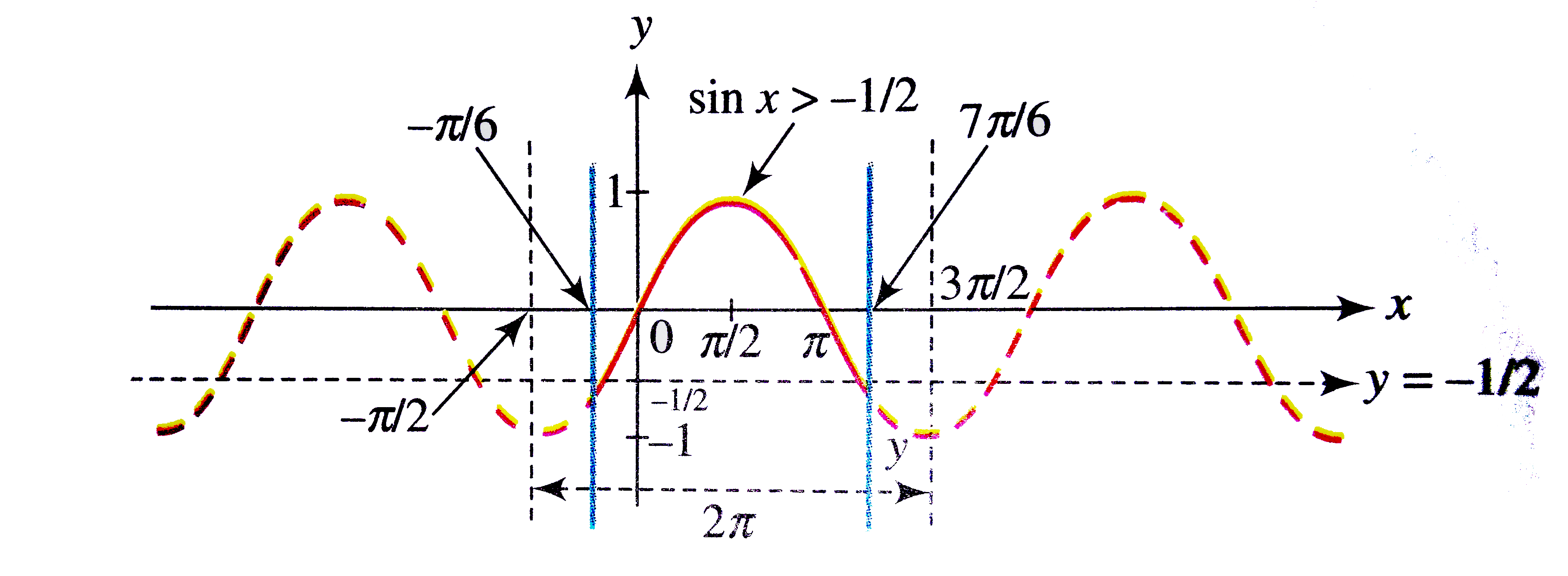
From the above figure, $sin x > - \frac{1}{2}$ when $- \frac{π}{6} < x < \frac{7 π}{6}$
Thus, on generalizing, the above solution becomes $2 n π - \frac{π}{6} < x < 2 n π + \frac{7 π}{6}, n \in Z$

Updated on:21/07/2023

Find the domain of
$f (x) = \sqrt{\frac{1 - | x |}{2 - | x |}}$ , is
A $(- \infty, \infty) - [- 2, 2]$
B $(- \infty, \infty) - [- 1, 1]$
C $[- 1, 1] \cup (- \infty, - 2) \cup (2, \infty)$
Dnone of these
The domain of $f (x) = 2 sin x + 3 cos x + 4$ is :
AR
B $R^{+}$
C $R - {0}$
D $R - {n π : n \in l^{+}}$
Domain of the function $f (x) = \sqrt{\frac{1}{sin x} - 1}$ is
A $U_{n \in 1} (2 n π, 2 n π + \frac{π}{2})$
B $U_{n \in 1} (2 n π, (2 n + 1) π]$
C $U_{n \in 1} [(2 n - 1) π, 2 n π]$
DNone of the above