Prove that $sin x + 2 x \geq \frac{3 x (x + 1)}{π}, \forall x \in [0, \frac{π}{2}]$ (Justify the inequality, if any used).

Video Solution

Text Solution

Verified by Experts

Let $f (x) = sin x + 2 x - \frac{3 x (x + 1)}{π}$
$∴$ $f' (x) = cos x + 2 - \frac{3}{π} (2 x + 1)$
Let $f' (x) = 0$
$∴$ $cos x = \frac{6}{π} x + \frac{3}{π} - 2$
Now draw the graphs of y = cos x and $y = \frac{6}{π} x + \frac{3}{π} - 2$ as shown in the following figure.

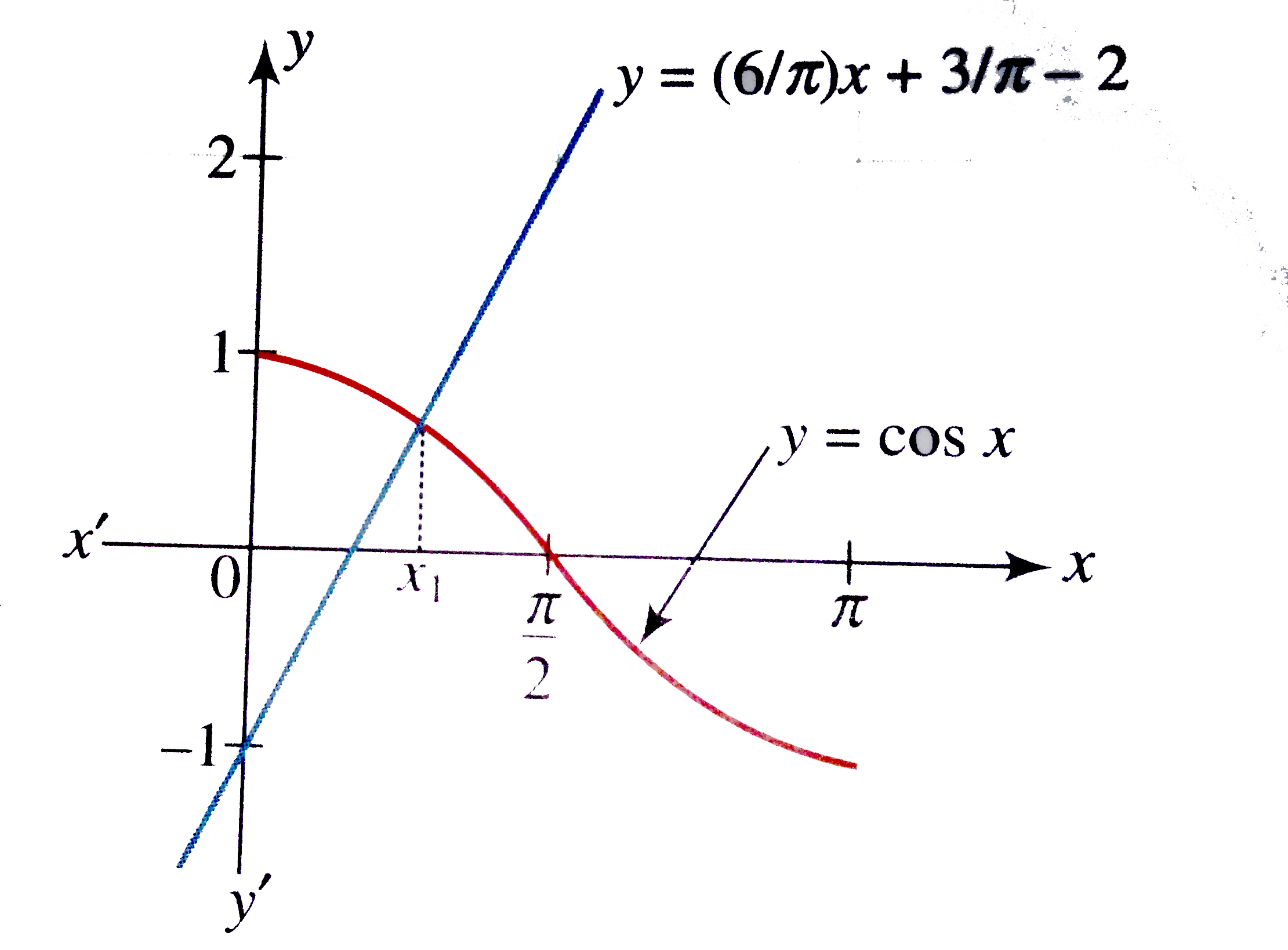
The graphs of y = cos x and $y = \frac{6}{π} x + \frac{3}{π} - 2$ intersect only once.
From the graph, $f' (x) = 0$ for some $x = x_{1} \in [0, \frac{π}{2}]$
For $x < x_{1}$ , the graph of y = cos x lies above the graph of $y = \frac{6}{π} x + \frac{3}{π} - 2$
For $x > x_{1}$ , the graph of y = cos x lies below the graph of $y = \frac{6}{π} x + \frac{3}{π} - 2$
Thus, $f' (x) > 0 for x < x_{1}$ , where f(x) increases, and $f' (x) < 0$ for $x > x_{1}$ , Where f(x) decreases.
Also $f'' (x) = - sin x - \frac{3}{π} (2) < 0$ , so the graph is concave downwards.
So $x = x_{1}$ is the point of maxima.
$f (0) = 0, f (\frac{π}{2}) = \frac{π}{4} - \frac{1}{2}$
Graph of y = f(x) is as shown in the following figure.

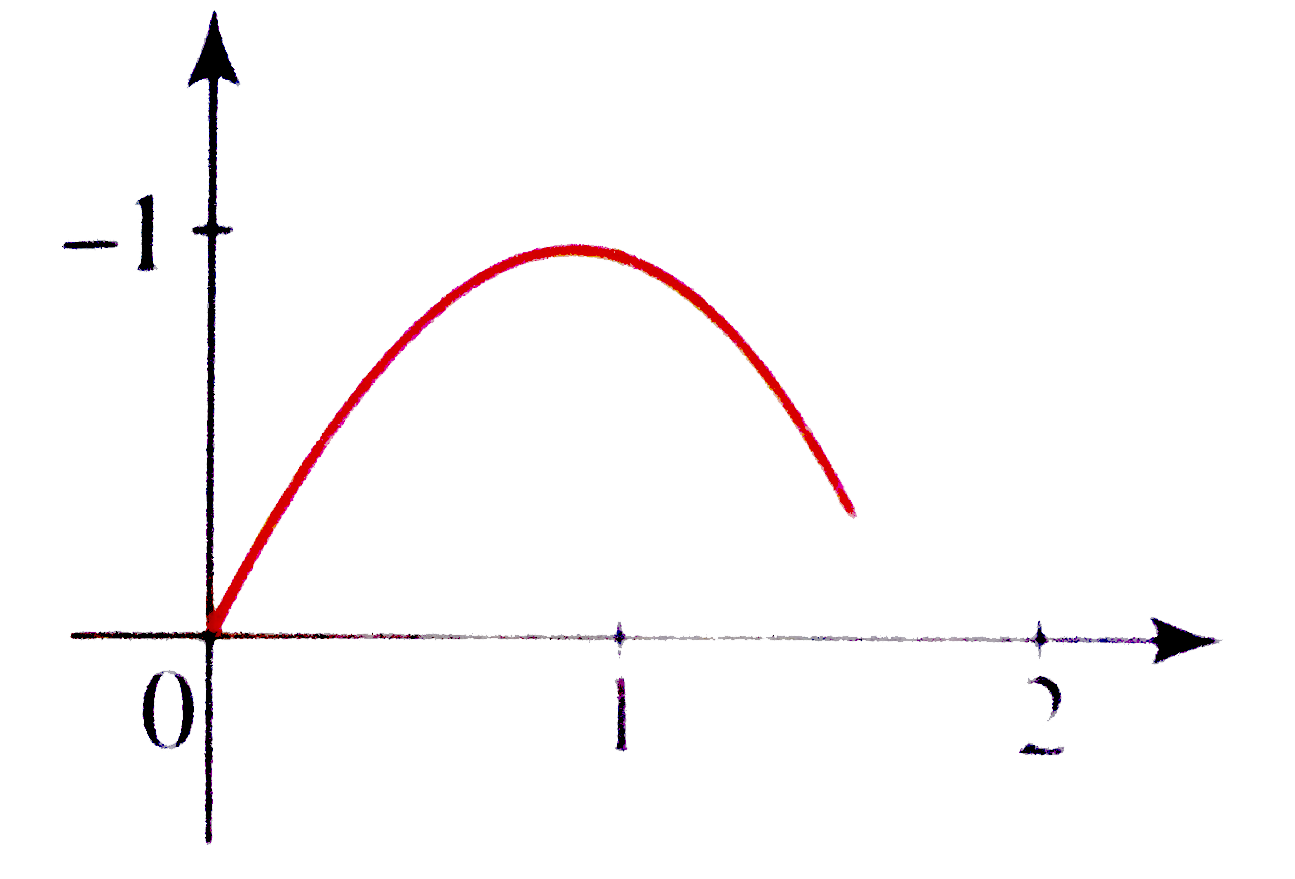
The graph lies completely above the x - axis, so $f (x) > 0 .$

Updated on:21/07/2023

If $sin x + x \geq | k | x^{2}, \forall x \in [0, \frac{π}{2}]$ , then the greatest value of k is
A $\frac{- 2 (2 + π)}{π^{2}}$
B $\frac{2 (2 + π)}{π^{2}}$
Ccan't be determined finitely
Dzero
If $f (x) = 2 sin x - x^{2}$ , then in $x \in [0, π]$
A $f (x)$ has no local maximum
B $f (x)$ has one local minimum
C $f (x)$ has 2 local maxima
D $f (x)$ has one local maximum