Find the values of a if equation 1−cosx=√32|x|xa,x∈(0,π), has exactly one solution.
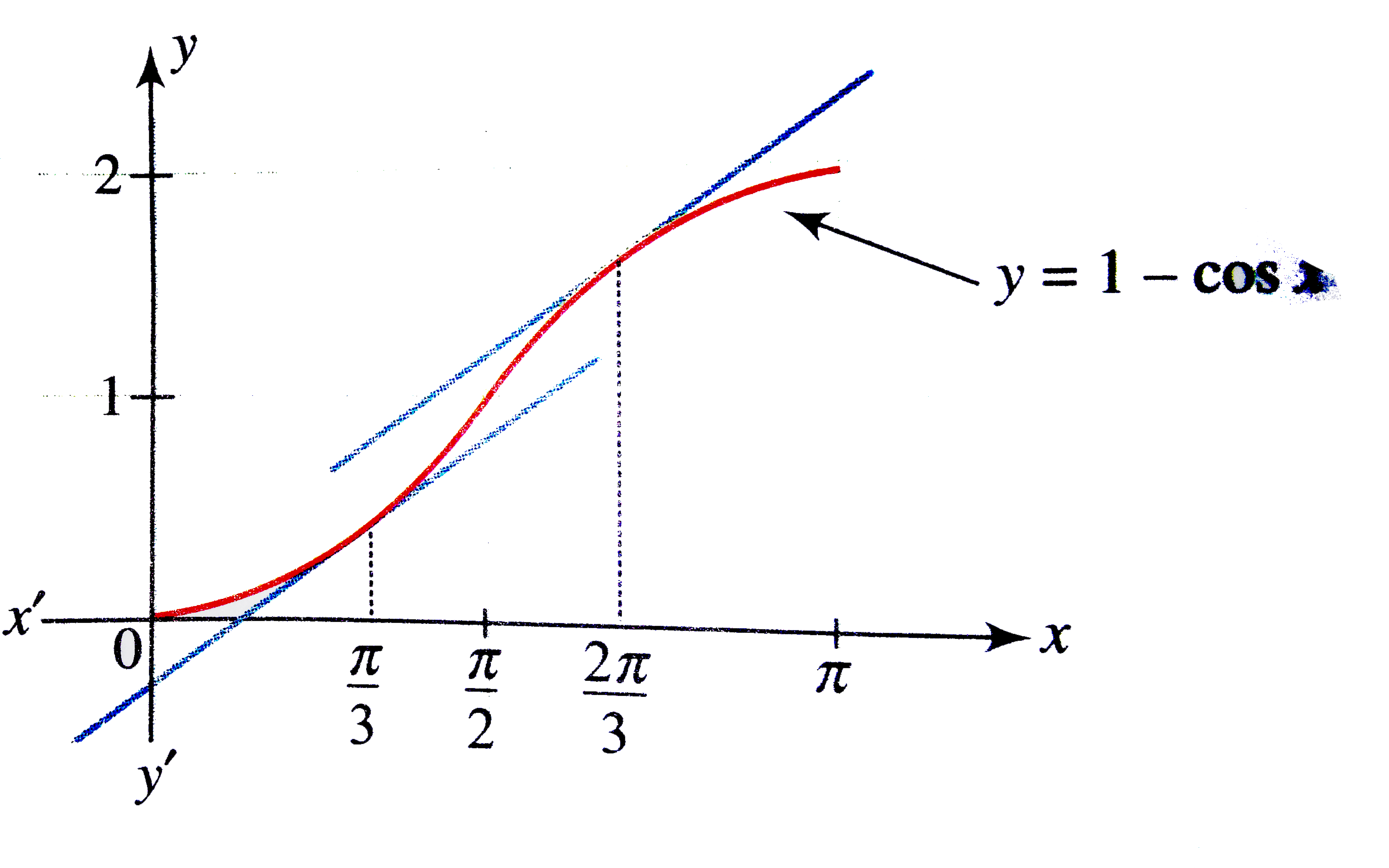
1−cosx=√32|x|+a has root when y=1−cosx and y=√32|x|+a intersect.
For one real solution, consider the case when two curves touch each other.
Slope of C1 is sin x and for x>0, slope of c2 is √32. Thus, for the point of contact,
sinx=√32⇒x=π3or2π3
Hence the point of contact is (π3,12)or(2π3,32)
For (π3,12), we get a=12−π2√3
For (2π3,32), we get a=32−π√3
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
Similar Questions
Find the values of a if equation 1−cosx=√32|x|+a,x∈(0,π), has exactly one solution.
View SolutionFind the values of x where function f(X)m=(sinx+cosx)(ex) in (0,2π) has point of inflection
View SolutionFind the possible values of p such that the equation px2=(log)ex has exactly one solution.
View SolutionFind the value of 'a' so that the equation f(x)=x2+(a−3)x+a=0 has exactly one α between the interval (1,2)andf(x+α)=0 has exactly one root between the interval (0,1)
View SolutionFind the value of 'a' so that the equation f(x)=x2+(a−3)x+a=0 has exactly one α between the interval (1,2)andf(x+α)=0 has exactly one root between the interval (0,1)
View SolutionFind the values of p so that the equation 2cos2x−(p+3)cosx+2(p−1)=0 has a real solution.
View SolutionFind the possible values of p such that the equation px2=lnx has exactly one solution.
View SolutionThe number of solution of √3Cos2x=(√3−1)Cosx+1,x∈[0,π2]
View SolutionThe number of integral values of n such that the equation 2n{x} = 3x + 2[x]has exactly 5 solutions.
View SolutionFind the number of solution of the equation √cos2x+2=(sinx+cosx) in [0,π].
View Solution
