If 0<α<π3, then prove that α(secα)<2π3.
Video Solution
Text Solution
Draw the graph of y = cos x for 1st quadrant .
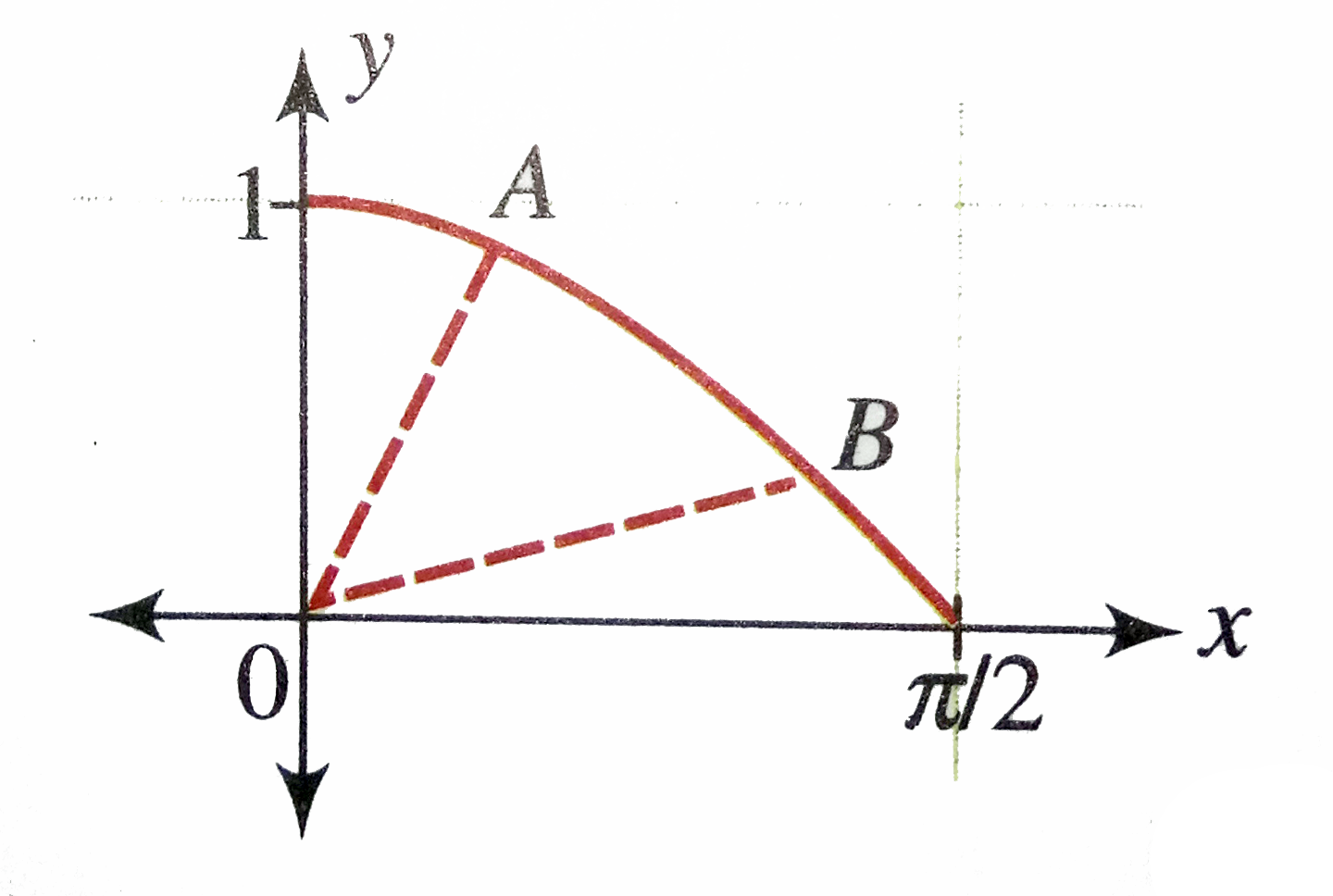
On the graph, let A≡(α,cosα),B≡(π3,cosπ3)
Clearly slope of OA> slope of OB
⇒ cosαα>cosπ3π3⇒αsecα<2π3
|
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBook:CENGAGEChapter:GRAPHS OF TRIGONOMETRIC FUNCTIONSExercise:Exercise
Explore 22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS Book:CENGAGEChapter:GRAPHS OF ELEMENTARY FUNCTIONS Exercise:Exercise
Explore 34 Videos
- HIGHT AND DISTANCE Book:CENGAGEChapter:HIGHT AND DISTANCE Exercise:JEE Previous Year
Explore 3 Videos
Similar Questions
Knowledge Check
If π2<α<3π4, then √2tanα+1cos2α is equal to
A−1+tanαB−1−tanαC1+tanαD1−tanαIf cosα=513and0<α<90∘, then the value of cotα+cosec α is
A2B3.5C4D1.5
If tanα=2 and 0<α<π2 then prove that x=a,π+α are the solution of the equation tan(2α−x)tan(2α+x)=11 that lies between 0 and 2π
View SolutionIf 0<α<π2 then show that tanα+cot>sinα+cosα
View SolutionIf α=2π7 prove that secα+sec2α+sec3α=−4.
View SolutionIf 0<α<π/16, then
(tanα+2tan(2α)+4tan(4α)+8cot(8α)cotα) is equal to
View Solution[ 7.If 0<α<β<π2 then [ 1)tanβtanα<αβ, 2) tanβtanα>αβ 3) tanαtanβ<αβ, 4) none ]]
View SolutionIf 0<α<β<π2 show that α−sinα<β−sinβ
View Solution

