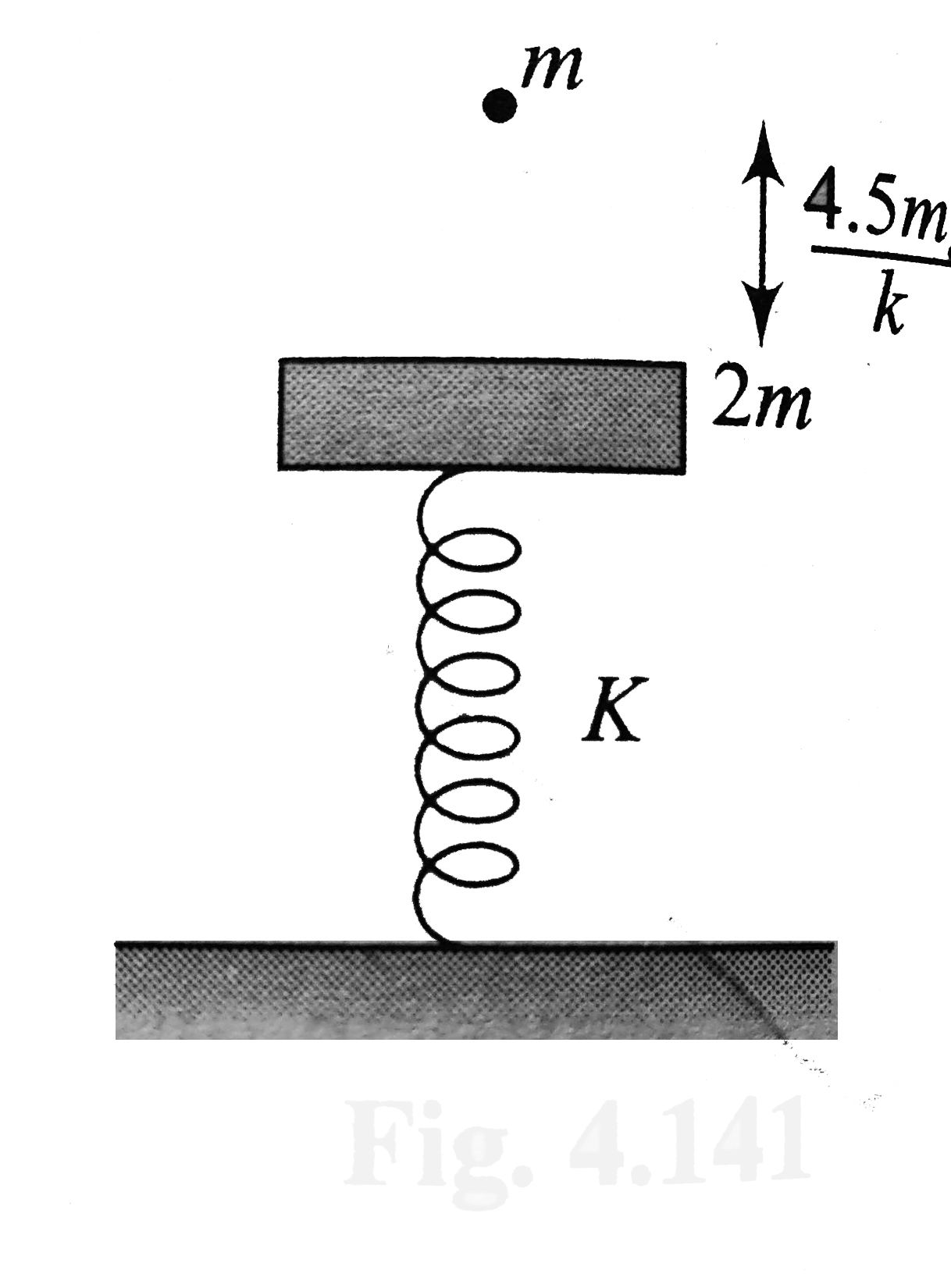
In the figure shown mass 2m is at rest and in equilibrium. A particle of mass m is released from height 4.5mgk from palte. The particle sticks to the plate. Neglecting the duration of collision. Starting form the when the particles sticks to plate to the time when the spring is in maximum compression for the first time is 2π√mak then find a.
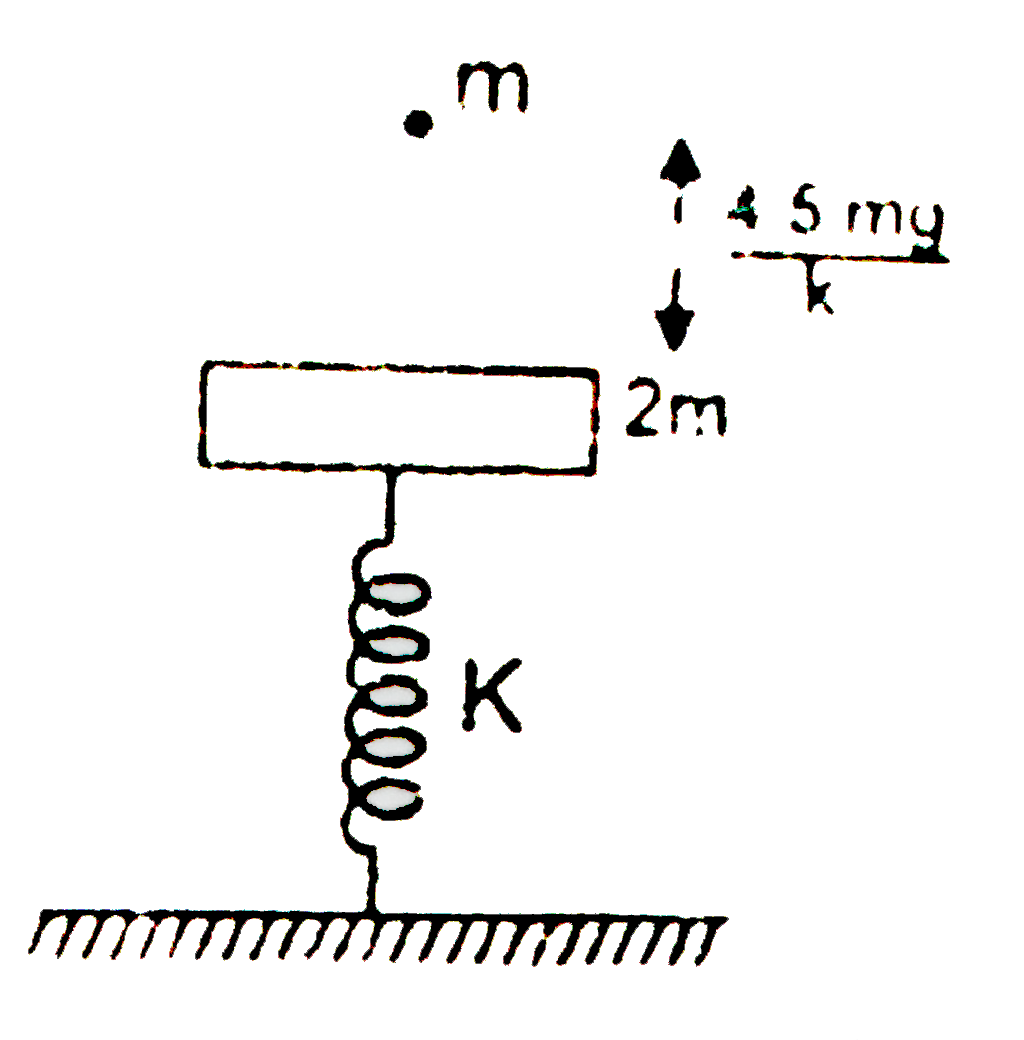
The correct Answer is:3
Velocity of the narticle just before collision
u=√2g×4.5mgK
u=3g√mK
Now it collides with the plate.
Now just after collision velocity of systeam of plate + particle
μ=3mv
⇒V=u3=g√mK
Now system perform 's SHM with time period T=2π√3mKand mean position as mgK distance below the point of collision.
Let the equation of motion be.
y=Asin(ωt+ϕ)
for t=0y=ng/K
mgK=Asinϕ....(1)
Now for amplitude
V=ω√A2−x2
g√mK=√K3m√A2−m2g2K2,(√3mgK)2=A2−m2g2K2
A=2mgK....(2)
By (1) & (2)
T=2π√3mK
X=A2 to x=0⇒t=T12
x=0 to x=A⇒t=T/4
total time =T12+T4=2π3√3mK=2π√m3k∴a=3
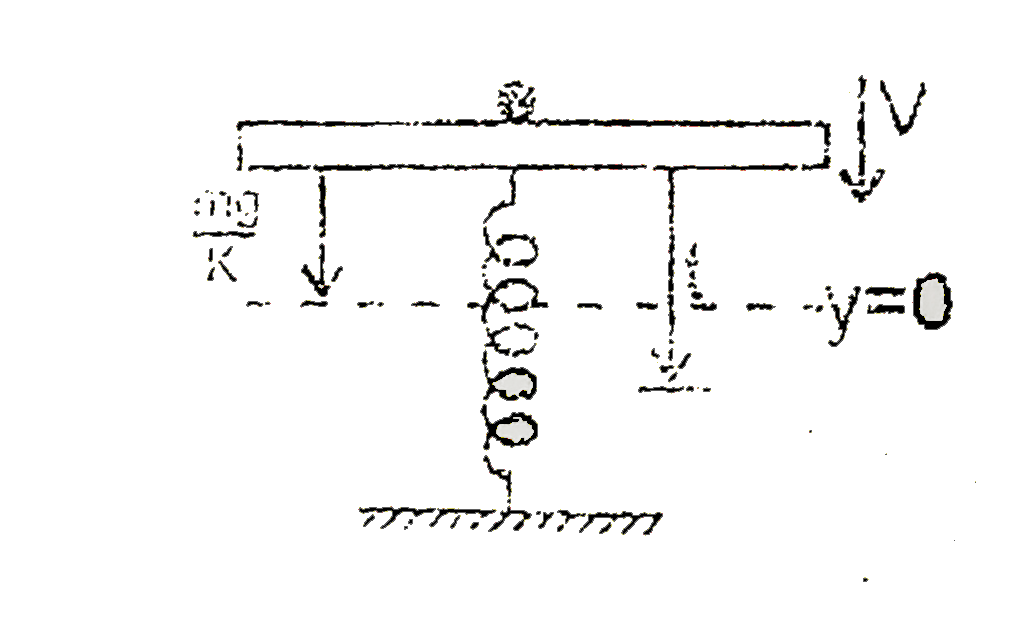
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - II
Explore 1 Video
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - III
Explore 12 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 1, PART - II
Explore 37 Videos
- SEMICONDUCTORSBook:RESONANCEChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:FST-3
Explore 30 Videos
Similar Questions
In the figure shown, mass 2m connected with a spring of force constant k is at rest and in equilibrium. A partical of mass m is released from height 4.5mg/k from 2m . The partical stick to the block. Neglecting the duration of collision find time from the release of m to the moment when the spring has maximum compression.
View SolutionA particle starts from rest. Its acceleration is varying with time as shown in the figure. When the particle comes to rest, its distance from its starting point is

View Solution
Knowledge Check
A particle of mass m is released from rest and follows a particle as a function of time?
 A
A B
B C
C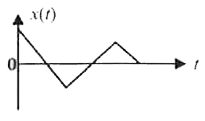 D
D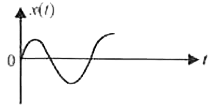
A massless platform is kept on a light elastic spring, as shown in the figure. When particle of mass 0.1 kg is dropped on the pan from a height of 0.24 m, the particle strikes the pan, and the spring is compressed by 0.01 m. From what height should the particle be dropped to cause a compression of 0.04 m?
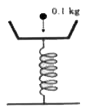 A0.96 mB2.96 mC3.96 mD0.48 m
A0.96 mB2.96 mC3.96 mD0.48 mA particle of mass m is driven by a machine that delivers a constant power k watts. If the particle starts from rest the force on the particle at time t is
A(√mk2)t−12B(√mk)t−12C(√2mk)t−12D(12√mk)t−12
In an ideal pulley particle system, mass m2 is connected with a vertical spring of stiffness k. If mass m2 is released from rest, when the spring is underformed, find the maximum compression of the spring.

View SolutionIn the example above, after how much time, particle comes to the starting point for the first time. (mass of particle = m)
View SolutionA particle of mass m is released from rest and follow a particle part as shown Assuming that the displacement of the mass from the origin is small which graph correctly depicts the position of the particle as a function of time?
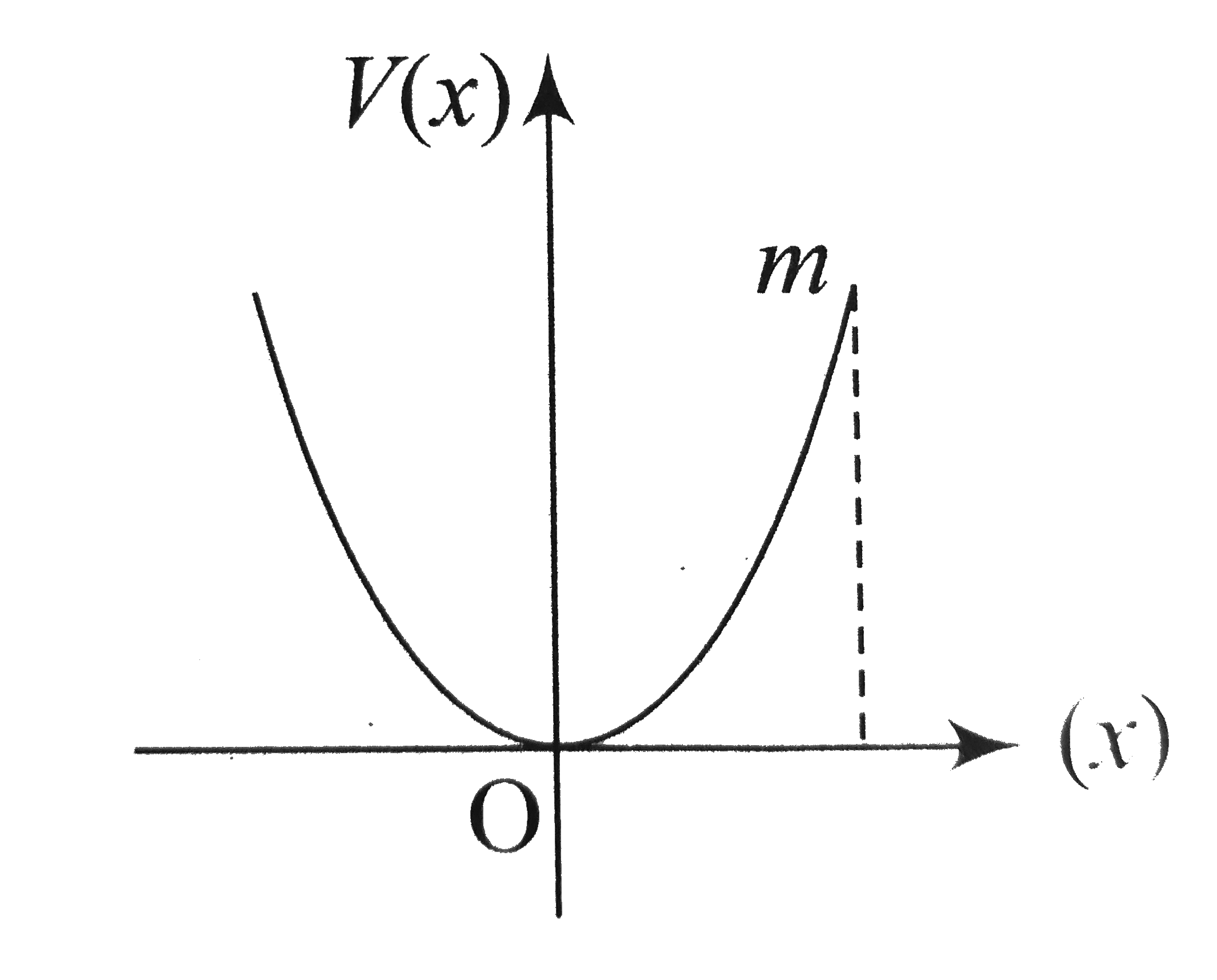
View SolutionIn the figure shown, the cart of mass 6m is initially at rest. A particle of mass m is attached to the end of the light rod which can rotate freely about A. If the rod is released from rest in a horizontal position shown, determine the velocity vrel of the particle with respect to the cart when the rod is vertical. (Assume frictionless surface)

View SolutionA particle of mass m is driven by a machine that delivers a constant power k watts. If the partilcle starts from rest the force on the particle at time t is
View Solution

